cspect

Arguments

x

vector, the data of the first signal.

y

vector, the data of the second signal. If y is omitted it is supposed to be equal to x (auto-correlation). If it is present, it must have the same number of element than x.

nx

a scalar : the number of points in the x signal. In this case the segments of the x signal are loaded by a user defined function named getx (see below).

ny

a scalar : the number of points in the y signal. In this case the segments of the y signal are loaded by a user defined function named gety (see below). If present ny must be equal to nx.

nlags

number of correlation lags (positive integer)

npoints

number of transform points (positive integer)

wtype

The window type

• 're': rectangular

• 'tr': triangular

• 'hm': Hamming

• 'hn': Hann

• 'kr': Kaiser,in this case the wpar argument must be given

• 'ch': Chebyshev, in this case the wpar argument must be given

wpar

optional parameters for Kaiser and Chebyshev windows:

• 'kr': wpar must be a strictly positive number

• 'ch': wpar must be a 2 element vector [main_lobe_width,side_lobe_height]with 0<main_lobe_width<.5, and side_lobe_height>0

sm

The power spectral estimate in the interval [0,1] of the normalized frequencies. It is a row array of size npoints. The array is real in case of auto-correlation and complex in case of cross-correlation.

cwp

the unspecified Chebyshev window parameter in case of Chebyshev windowing, or an empty matrix.

Description

Computes the cross-spectrum estimate of two signals x and y if both are given and the auto-spectral estimate of x otherwise. Spectral estimate obtained using the correlation method.

The cross spectrum of two signal x and y is defined to be

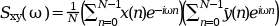
The correlation method calculates the spectral estimate as the Fourier transform of a modified estimate of the auto/cross correlation function. This auto/cross correlation modified estimate consist of repeatedly calculating estimates of the autocorrelation function from overlapping sub-segments if the data, and then averaging these estimates to obtain the result.

The number of points of the window is 2*nlags-1.

For batch processing, thex and y data may be read segment by segment using the getxand gety user defined functions. These functions have the following syntax:

xk=getx(ns,offset) and yk=gety(ns,offset) where ns is the segment size and offset is the index of the first element of the segment in the full signal.

Warning

For Scilab version up to 5.0.2 the returned value was the modulus of the current one.

Reference

Oppenheim, A.V., and R.W. Schafer. Discrete-Time Signal Processing, Upper Saddle River, NJ: Prentice-Hall, 1999

Examples

rand('normal');rand('seed',0);
x=rand(1:1024-33+1);
//make low-pass filter with eqfir
nf=33;bedge=[0 .1;.125 .5];des=[1 0];wate=[1 1];
h=eqfir(nf,bedge,des,wate);
//filter white data to obtain colored data
h1=[h 0*ones(1:max(size(x))-1)];
x1=[x 0*ones(1:max(size(h))-1)];
hf=fft(h1,-1);   xf=fft(x1,-1);yf=hf.*xf;y=real(fft(yf,1));
sm=cspect(100,200,'tr',y);
smsize=max(size(sm));fr=(1:smsize)/smsize;
plot(fr,log(sm))

See also

• pspect — two sided cross-spectral estimate between 2 discrete time signals using the Welch's average periodogram method.
• mese — maximum entropy spectral estimation
• corr — корреляция, ковариация