Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
semidef
Solve semidefinite problems.
Syntax
x=semidef(x0,Z0,F,blocksizes,c,options) [x,Z]=semidef(...) [x,Z,ul]=semidef(...) [x,Z,ul,info]=semidef(...)
Arguments
- x0
m-by-1 real column vector (must be strictly primal feasible, see below)
- Z0
L-by-1 real vector (compressed form of a strictly feasible dual matrix, see below)
- F
L-by-(m+1) real matrix
- blocksizes
p-by-2 integer matrix (sizes of the blocks) defining the dimensions of the (square) diagonal blocks
size(Fi(j)=blocksizes(j) j=1,...,m+1.- c
m-by-1 real vector
- options
a 1-by-5 matrix of doubles
[nu,abstol,reltol,tv,maxiters]- ul
a 1-by-2 matrix of doubles.
Description
semidef solves the semidefinite program:

and its dual:
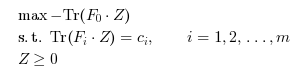
exploiting block structure in the matrices
F_i.
Here, Tr is the trace operator, i.e. the sum of the
diagonal entries of the matrix.
The problem data are the vector c and m+1
block-diagonal symmetric matrices F0, F1,
..., Fm.
Moreover, we assume that the matrices Fi have
L diagonal blocks.
The Fi's matrices are stored columnwise in
F in compressed format: if F_i^j,
i=0,..,m, j=1,...,L denote the jth (symmetric) diagonal block of
F_i, then
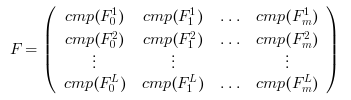
where, for each symmetric block M, the vector cmp(M) is
the compressed representation of M, that is
[M(1,1);M(1,2);...;M(1,n);M(2,2);M(2,3);...;M(2,n);...;M(n,n)],
obtained by scanning rowwise the upper triangular part of
M.
For example, the matrix

is stored as
[1; 2; 3; 4; 5; 6; 7; 8; 9; 10]
with blocksizes=[2,3,1].
In order to create the matrix F, the user can combine the
list2vec and pack function, as described in the example below.
blocksizes gives the size of block
j, ie,
size(F_i^j)=blocksizes(j).
Z is a block diagonal matrix with L blocks Z^0, ...,
Z^{L-1}
.Z^j has size blocksizes[j]
times blocksizes[j]
.Every block is stored using packed storage of
the lower triangular part.
The 1-by-2 matrix of doubles ul contains the primal objective
value c'*x and the dual objective value
-trace(F_0*Z).
The entries of options are respectively:
nu: a real parameter which controls the rate of convergence.abstol: absolute tolerance. The absolute tolerance cannot be lower than 1.0e-8, that is, the absolute tolerance used in the algorithm is the maximum of the user-defined tolerance and the constant tolerance 1.0e-8.reltol: relative tolerance (has a special meaning when negative).tv: the target value, only referenced ifreltol < 0.maxiters: the maximum number of iterations, a positive integer value.
On output, the info variable contains the status of the execution.
info=1if maxiters exceeded,info=2if absolute accuracy is reached,info=3if relative accuracy is reached,info=4if target value is reached,info=5if target value is not achievable;negative values indicate errors.
Convergence criterion is based on the following conditions that is, the algorithm stops if one of the following conditions is true:
maxiters is exceeded
duality gap is less than abstol
primal and dual objective are both positive and duality gap is less than (
reltol* dual objective) or primal and dual objective are both negative and duality gap is less than (reltol* minus the primal objective)reltol is negative and primal objective is less than tv or dual objective is greater than
tv.
Examples
// 1. Define the initial guess x0=[0;0]; // // 2. Create a compressed representation of F // Define 3 symmetric block-diagonal matrices: F0, F1, F2 F0=[2,1,0,0; 1,2,0,0; 0,0,3,1; 0,0,1,3] F1=[1,2,0,0; 2,1,0,0; 0,0,1,3; 0,0,3,1] F2=[2,2,0,0; 2,2,0,0; 0,0,3,4; 0,0,4,4] // Define the size of the two blocks: // the first block has size 2, // the second block has size 2. blocksizes=[2,2]; // Extract the two blocks of the matrices. F01=F0(1:2,1:2); F02=F0(3:4,3:4); F11=F1(1:2,1:2); F12=F1(3:4,3:4); F21=F2(1:2,1:2); F22=F2(3:4,3:4); // Create 3 column vectors, containing nonzero entries // in F0, F1, F2. F0nnz = list2vec(list(F01,F02)); F1nnz = list2vec(list(F11,F12)); F2nnz = list2vec(list(F21,F22)); // Create a 16-by-3 matrix, representing the // nonzero entries of the 3 matrices F0, F1, F2. FF=[F0nnz,F1nnz,F2nnz] // Compress FF CFF = pack(FF,blocksizes); // // 3. Create a compressed representation of Z // Create the matrix Z0 Z0=2*F0; // Extract the two blocks of the matrix Z01=Z0(1:2,1:2); Z02=Z0(3:4,3:4); // Create 2 column vectors, containing nonzero entries // in Z0. ZZ0 = [Z01(:);Z02(:)]; // Compress ZZO CZZ0 = pack(ZZ0,blocksizes); // // 4. Create the linear vector c c=[trace(F1*Z0);trace(F2*Z0)]; // // 5. Define the algorithm options options=[10,1.d-10,1.d-10,0,50]; // 6. Solve the problem [x,CZ,ul,info]=semidef(x0,CZZ0,CFF,blocksizes,c,options) // // 7. Check the output // Unpack CZ Z=unpack(CZ,blocksizes); w=vec2list(Z,[blocksizes;blocksizes]); Z=blockdiag(w(1),w(2)) c'*x+trace(F0*Z) // Check that the eigenvalues of the matrix are positive spec(F0+F1*x(1)+F2*x(2)) trace(F1*Z)-c(1) trace(F2*Z)-c(2)
Implementation notes
This function is based on L. Vandenberghe and S. Boyd sp.c program.
References
L. Vandenberghe and S. Boyd, " Semidefinite Programming," Informations Systems Laboratory, Stanford University, 1994.
Ju. E. Nesterov and M. J. Todd, "Self-Scaled Cones and Interior-Point Methods in Nonlinear Programming," Working Paper, CORE, Catholic University of Louvain, Louvain-la-Neuve, Belgium, April 1994.
SP: Software for Semidefinite Programming, User's Guide, Beta Version, November 1994, L. Vandenberghe and S. Boyd, 1994 http://www.ee.ucla.edu/~vandenbe/sp.html
| Report an issue | ||
| << recons | Semidefinite Programming | unpack >> |