Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
Sigbuilder
Signal creator/generator
Block Screenshot
Contents
Description
The Signal Builder block is a superblock containing a block whose output event port is connected to its input event port. This event feedback gives the possibility to generate events at discontinuous point of the signal. The generated events automatically restart the numerical solver and avoids numerical problems. The generated event is also made available to the user for possible use. Remind that if higher interpolation methods are used, the events are generated only at the beginning and at the end of the signal.
Parameters
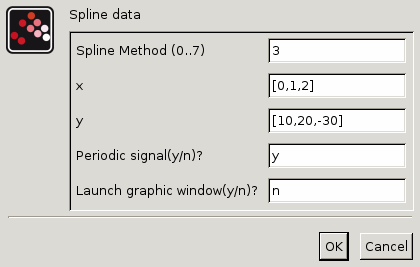
Spline method (0…7) : Accepted values are 0, 1, 2, 3, 4, 5, 6 or 7. This parameter defines the spline method for interpolating the points. The Signal builder block computes a linear or a cubic spline or sub-spline S which interpolates the (xi,yi) points, i.e., we have S(xi) = yi for all i=1,…,n. Available methods are described here-below:
0 : "Zero order method". This method generates a piecewise constant signal. i.e., for ti ≤ t < ti+1, y(t) = yi. This method is available for all data types.
Linear method. This method generates a piecewise linear signal, i.e., for ti ≤ t < ti+1, y(t) = yi + (yi+1 - yi) (t - ti) / (ti+1 - ti).
NATURAL method. The interpolation is done by passing 2-order polynomials between (xi, yi) and (xi+1, yi+1). The Derivative at (xi, yi) is identical for two adjacent polynomials. The derivative at (x1, y1) can be selected arbitrary: It is selected such that the sum of derivatives at all points be minimum. This condition provides a less fluctuated signal.
NOT_A_KNOT method. The cubic spline is computed by using the following conditions (considering n points xi, …, xn) :
S(3) (x2-) = S(3) (x2+) S(3) (xn-1-) = S(3) (xn-1+) Periodic. A periodic cubic spline is computed (y must verify y1=yn) by using the conditions: xi, …, xn :
S′(x1) = S′(xn) S″(x1) = S″(xn) In this case, the value of yn is ignored and y1 is used instead. Note that, in order to generate a periodic signal, the Periodic flag must be activated.
Monotone. In this case a sub-spline (S is only 1-continuously differentiable) is computed such that S is monotone on each interval:
- if yi ≤ yi+1 : S is increasing on [xi, xi+1]
- Otherwise: S is decreasing on [xi, xi+1]
Clamped. In this case, the cubic spline S is computed by using the end points derivatives which are set to zero, i.e.
S′(x1) = S′(xn) = 0 Fast. In this case, a sub-spline is computed by using a simple local scheme for the derivative at xi of the interpolation polynomial of [ (xi-1, yi-1), (xi, yi), (xi+1, yi+1) ], except for the end points (derivative at these points are computed from the 3 left most points and the 3 right most points).
x : Row or column vector of abscissae (X-axis), as decimal numbers. This vector can be also defined in the Scicos context. It can be specified by a Scilab expression.
y : Row or column vector of ordinates (Y-axis), as decimal numbers. This vector can be also defined in the Scicos context. It can be specified by a Scilab expression.
Periodic signal (y/n): If
yis selected, the created signal will be periodic with the period of tn. Note that if the Periodic spline method is selected, the output signal will be a continuous signal. Otherwise, the signal will be discontinuous at endpoints.Launch graphical window (y/n): If
yis selected, clicking on theOKbutton opens a graphical window, in whch the user can edit data points:Mouse left click on the window : Adds a new data point Mouse right click on the window : Removes a data point. Mouse left double-click on a data point : Edits a point's coordinates Mouse left button press/drag/release : Moves a data point Autoscale menu : Rescales the window to show all data points properly. Spline/Method menu : Selects the spline interpolation method. Data/Clear menu : Removes all data points. Data/Data_Bounds menu : Changes the window size. Data/Load_from_text_file menu : Reads data points from a text data file (using C data format). Data/save_to_text_file menu : Saves the data points to a text data file (using C data format). Data/Load_from_excel menu : Reads data from an excel file. Data/Periodic_signal menu : Specifies weather the created signal is periodic or not. If the signal is not periodic, the signal stays constant beyond tn. Otherwise it is clamped to y1 at tn. Standards/Functions menu : Chooses a Sine, Sawtooth, Pulse, or random signal. Exit/Help menu : Short help on the graphic window commands. Exit/Exit_without_save menu : Closes the graphical window, discarding all modifications in data. Exit/Exit_with_save menu : Closes the graphical window and saving data points.
Default properties
always active: no
direct-feedthrough: no
zero-crossing: no
mode: no
regular outputs:
- port 1 : size [-1,1] / type 1
number/sizes of activation inputs: 0
number/sizes of activation outputs: 1
continuous-time state: no
discrete-time state: no
object discrete-time state: no
name of computational function: csuper
Interfacing function
SCI/modules/scicos_blocks/macros/Sources/Sigbuilder.sci
| Report an issue | ||
| << SAWTOOTH_f | Palette Sources | STEP_FUNCTION >> |