Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
DLR
Discrete transfer function
Block Screenshot
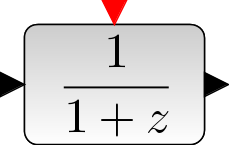
Description
This block realizes a SISO linear system represented by its rational transfer function (in the symbolic variable z). The rational function must be proper.
Parameters

Numerator (z)
This parameter sets the numerator of the transfer function.
This must be a polynomial inz .
Properties : Type 'pol' of size 1.
 In the provided expression, any subexpression being an exponent given either by a variable (of the context) whose name is more than 1-character long, or by an expression (not a literal integer) must end with a space to be correctly displayed on the block's icon. This constrain has no consequence on the computational validity of the expression. Examples: "z^12+1", "z^ +12+1", "z^+ 12+1" are all displayed as "z^{12}+1", while "1+z^ab+z^2" will be displayed as "1+z^{ab+z^2}" (but will be well computed as
In the provided expression, any subexpression being an exponent given either by a variable (of the context) whose name is more than 1-character long, or by an expression (not a literal integer) must end with a space to be correctly displayed on the block's icon. This constrain has no consequence on the computational validity of the expression. Examples: "z^12+1", "z^ +12+1", "z^+ 12+1" are all displayed as "z^{12}+1", while "1+z^ab+z^2" will be displayed as "1+z^{ab+z^2}" (but will be well computed as1 + z^ab + z^2). To make it well displayed, "1+z^ab +z^2" will have to be entered (for instance). As well, "z^(ab+1) + 2" will have to be entered, instead of "z^(ab+1)+2".Denominator (z)
This parameter sets the denominator of the transfer function.
This must be a polynomial inz .
Properties : Type 'pol' of size 1.
Take care about multichar exponents (see
Numerator).
Default properties
always active: no
direct-feedthrough: no
zero-crossing: no
mode: no
regular inputs:
- port 1 : size [1,1] / type 1
regular outputs:
- port 1 : size [1,1] / type 1
number/sizes of activation inputs: 1
number/sizes of activation outputs: 0
continuous-time state: no
discrete-time state: yes
object discrete-time state: no
name of computational function: dsslti4
Interfacing function
SCI/modules/scicos_blocks/macros/Linear/DLR.sci
Computational function
SCI/modules/scicos_blocks/src/c/dsslti4.c (Type 4)
| Report an issue | ||
| << DELAY_f | Discrete time systems palette | DLRADAPT_f >> |