Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
DDaskr
Double-precision Differential Algebraic equations system Solver with Krylov method and Rootfinding: numerical solver providing an efficient and stable method to solve Differential Algebraic Equations systems (DAEs) Initial Value Problems
Description
Called by xcos, DDaskr (short for Double-precision Differential Algebraic equations system Solver with Krylov method and Rootfinding) is a numerical solver providing an efficient and stable method to solve Initial Value Problems of the form:
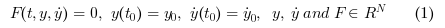
Starting then with those y0 and yPrime0 , DDaskr approximates yn+1 with the BDF formula:
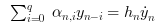
with, like in CVode, yn the approximation of y(tn) , hn = tn - tn-1 the step size, and the coefficients are fixed, uniquely determined by the method type, its order q ranging from 1 to 5 and the history of the step sizes.
Injecting this formula in (1) yields the system:
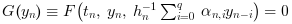
Its solving is done through a Newton method, but with either direct or preconditioned GMRes Krylov iterations.
Direct iteration: start by rewriting the system into:
![J \left[y_{n(m+1)}-y_{n(m)} \right] = -G(y_{n(m)})](/docs/6.0.2/pt_BR/_LaTeX_7-DDaskr.xml_4.png)
with J an approximation of the Jacobian:
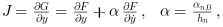
α changes whenever the step size or the method order varies.
Then, an implemented direct dense solver is used and we go on to the next step.
GMRes Krylov method: first, precondition the system by applying the Jacobian matrix mentioned above.
Secondly, compute the next Krylov space basis and update the Hessenberg matrix.
Test for convergence for the first time. If it doesn't pass, calculate the residual, which will lead to a new potential solution, and iterate until that residual satisfies convergence.
DDaskr uses the history array to control the local error yn(m) - yn(0) and recomputes hn if that error is not satisfying.
The function is called in between activations, because a discrete activation may change the system.
Following the criticality of the event (its effect on the continuous problem), we either relaunch the solver with different start and final times as if nothing happened, or, if the system has been modified, we need to "cold-restart" the problem by reinitializing it anew and relaunching the solver.
Averagely, DDaskr accepts tolerances up to 10-11. Beyond that, it returns a Too much accuracy requested error.
As of now, DDaskr can only be applied on systems where the root functions are punctually 0, and not 0-flat.
Example
The 'Modelica Generic' block returns its continuous states, we can evaluate them with DDaskr by running the example:
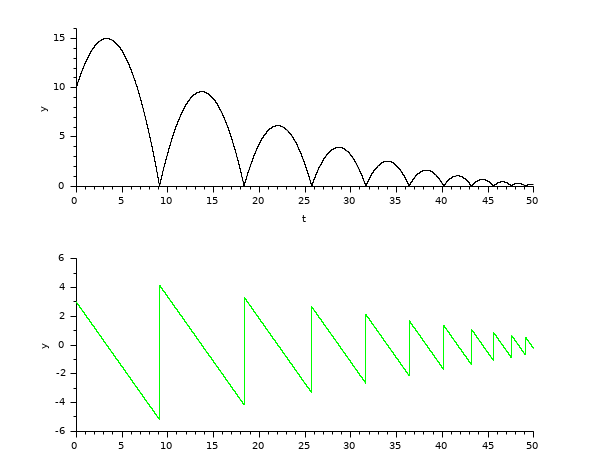
See also
- LSodar — LSodar (short for Livermore Solver for Ordinary Differential equations, with Automatic method switching for stiff and nonstiff problems, and with Root-finding) is a numerical solver providing an efficient and stable method to solve Ordinary Differential Equations (ODEs) Initial Value Problems.
- CVode — CVode (short for C-language Variable-coefficients ODE solver) is a numerical solver providing an efficient and stable method to solve Ordinary Differential Equations (ODEs) Initial Value Problems. It uses either BDF or Adams as implicit integration method, and Newton or Functional iterations.
- IDA — Implicit Differential Algebraic equations system solver, providing an efficient and stable method to solve Differential Algebraic Equations system (DAEs) Initial Value Problems.
- Runge-Kutta 4(5) — Runge-Kutta is a numerical solver providing an efficient explicit method to solve Ordinary Differential Equations (ODEs) Initial Value Problems.
- Dormand-Prince 4(5) — Dormand-Prince is a numerical solver providing an efficient explicit method to solve Ordinary Differential Equations (ODEs) Initial Value Problems.
- Implicit Runge-Kutta 4(5) — Numerical solver providing an efficient and stable implicit method to solve Ordinary Differential Equations (ODEs) Initial Value Problems.
- Crank-Nicolson 2(3) — Crank-Nicolson is a numerical solver based on the Runge-Kutta scheme providing an efficient and stable implicit method to solve Ordinary Differential Equations (ODEs) Initial Value Problems. Called by xcos.
- Comparisons — This page compares solvers to determine which one is best fitted for the studied problem.
- daskr — DAE solver with zero crossing
- ode — Solucionador de equações diferenciais ordinárias
- ode_discrete — solucionador de equações diferenciais ordinárias, simulação de tempo discreto
- ode_root — solucionador de EDOs com busca de raízes
- odedc — solucionador de EDOs contínuas/discretas
- impl — equações diferenciais algébricas
History
| Versão | Descrição |
| 5.5.0 | DDaskr solver added |
| Report an issue | ||
| << IDA | Solvers | Rootfinding >> |