Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
cov
Covariance matrix
Syntax
C = cov(x) C = cov(x, 0) C = cov(x, 1) C = cov(x, y) C = cov(x, y, 0) C = cov(x, y, 1)
Parameters
- x
a nobs-by-1 or nobs-by-nvar matrix of doubles
- y
a nobs-by-1 or nobs-by-nvar matrix of doubles
- C
a square matrix of doubles, the empirical covariance
Description
If x is a nobs-by-1 matrix,
then cov(x) returns the variance of x,
normalized by nobs-1.
If x is a nobs-by-nvar matrix,
then cov(x) returns the nvar-by-nvar covariance matrix of the
columns of x, normalized by nobs-1.
Here, each column of x is a variable and
each row of x is an observation.
If x and y are two nobs-by-1 matrices,
then cov(x, y) returns the 2-by-2 covariance matrix of x and
y, normalized by nobs-1, where nobs is the number of observations.
cov(x, 0) is the same as cov(x) and
cov(x, y, 0) is the same as cov(x, y).
In this case, if the population is from a normal distribution,
then C is the best unbiased estimate of the covariance matrix.
cov(x, 1) and cov(x, y, 1) normalize by nobs.
In this case, C is the second moment matrix of the
observations about their mean.
The covariance of X and Y is defined by:
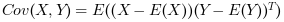
where E is the expectation.
This function is compatible with Matlab.
Examples
x = [1; 2]; y = [3; 4]; C = cov(x, y) expected = [0.5, 0.5; 0.5, 0.5]; C = cov([x, y])
x = [230; 181; 165; 150; 97; 192; 181; 189; 172; 170]; y = [125; 99; 97; 115; 120; 100; 80; 90; 95; 125]; expected = [ 1152.4556, -88.911111 -88.911111, 244.26667 ]; C = cov(x, y) C = cov([x, y])
// Source [3] A = [ 4.0 2.0 0.60 4.2 2.1 0.59 3.9 2.0 0.58 4.3 2.1 0.62 4.1 2.2 0.63 ]; S = [ 0.025 0.0075 0.00175 0.0075 0.007 0.00135 0.00175 0.00135 0.00043 ]; C = cov(A)
Bibliography
[3] NIST/SEMATECH e-Handbook of Statistical Methods, 6.5.4.1. Mean Vector and Covariance Matrix
"Introduction to probability and statistics for engineers and scientists", Sheldon Ross
History
| Version | Description |
| 5.5.0 | cov function added, to improve mvvacov (deprecated) |
| Report an issue | ||
| << correl | Descriptive Statistics | covar >> |