- Aide de Scilab
- Graphiques
- 2d_plot
- champ
- champ1
- champ properties
- comet
- contour2d
- contour2di
- contour2dm
- contourf
- errbar
- fchamp
- fec
- fec properties
- fgrayplot
- fplot2d
- grayplot
- grayplot properties
- graypolarplot
- histplot
- LineSpec
- Matplot
- Matplot1
- Matplot properties
- paramfplot2d
- plot
- plot2d
- plot2d2
- plot2d3
- plot2d4
- polarplot
- scatter
- Sfgrayplot
- Sgrayplot
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
contour2dm
compute level curves of a surface defined with a mesh
Syntax
[xc, yc] = contour2dm(x, y, polygons, func, nz)
Arguments
- x, y
two vectors of size
n,(x(i),y(i))gives the coordinates of nodei.- polygons
is a
[Ntr,N+2]matrix. Each line ofpolygonsspecifies a convex polygon of the meshpolygons(j) = [number,node1,node2,node3, ..., nodeN, flag].node1,node2,node3, ..., nodeNare the number of the nodes which constitutes the polygon. number is the number of the polygons and flag is an integer not used in thecontour2dmfunction.- func
a vector of size
n:func(i)gives the value at nodeiof the function.- nz
the level values or the number of levels.
- If
nzis an integer its value gives the number of level curves equally spaced from
zmintozmaxas follows:z= zmin + (1:nz)*(zmax-zmin)/(nz+1)
- If
nzis a vector nz(i)gives the value of thei-th level curve.
- If
- xc, yc
vectors of identical sizes containing the contours definitions. See below for details.
Description
contour2dm computes level curves of a surface
z = f(x, y) on a 2D plot. The values of
f(x,y) are given by the matrix z
at the points of the mesh defined by x and y.
xc(1) contains the level associated with first
contour path, yc(1) contains the number
N1 of points defining this contour path and
(xc(1+(1:N1)), yc(1+(1:N1)) )
contain the coordinates of the paths points. The second path begin
at xc(2+N1) and yc(2+N1) and
so on.
Note that some loops can appear on a level curve when some vertexes of polygons as the same value as the level one. See example #2
Examples
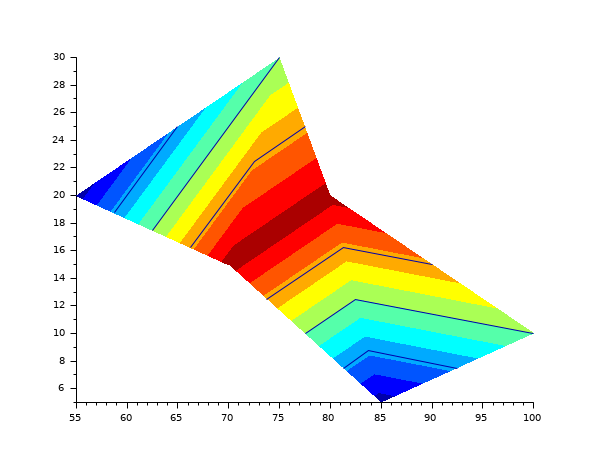
m = [6 5 4; ... 6 2 5; ... 6 4 1; ... 5 2 3]; nodes = [55 20; ... 85 5; ... 100 10; ... 75 30; ... 80 20; ... 70 15]; z_fec = [-1 -1 0 0 1 1]; f = scf(); f.color_map = jetcolormap(12); fec(nodes(:, 1), nodes(:, 2), [(1:size(m, 1))', m, (1:size(m, 1))'], z_fec); [xc, yc] = contour2dm(nodes(:,1), nodes(:,2), [(1:size(m, 1))', m, (1:size(m, 1))'], z_fec, [-0.5, 0, 0.5]); k=1;n=yc(k);c=1; N = size(xc, '*') while k <= N & k+yc(k)<=N n=yc(k); plot2d(xc(k+(1:n)),yc(k+(1:n))); c=c+1; k=k+n+1; end
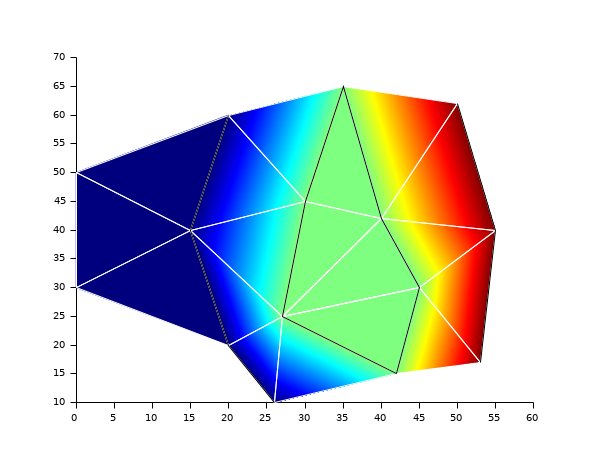
f=scf(); f.color_map = jetcolormap(3); m = [1 2 3; ... 1 3 4; ... 3 4 5; ... 6 2 3; ... 7 6 3; ... 7 3 5; ... 7 5 8; ... 2 9 6; ... 9 6 10; ... 6 7 10; ... 10 11 7; ... 7 8 12; ... 9 10 13; ... 7 10 11; ... 7 12 11; ... 13 10 14; ... 10 11 14; ... 11 14 15; ... 11 12 15]; nodes = [0 50; ... //1 20 60; ... //2 15 40; ... //3 0 30; ... //4 20 20; ... //5 30 45; ... //6 27 25; ... //7 26 10; ... //8 35 65; ... //9 40 42; ... //10 45 30; ... //11 42 15; ... //12 50 62; ... //13 55 40; ... //14 53 17]; //15 z = [0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 2, 2, 2]; nb_mesh = [(1:size(m, 1))', m, (1:size(m, 1))']; fec(nodes(:, 1), nodes(:, 2), nb_mesh, z, mesh=%t); e=gce(); e.children.foreground = -2; // Contour2dm [xc, yc] = contour2dm(nodes(:,1), nodes(:,2), nb_mesh, z, linspace(0,3,4)); k=1;n=yc(k);c=1; N = size(xc, '*'); while k <= N & k+yc(k)<=N n=yc(k); plot2d(xc(k+(1:n)),yc(k+(1:n))); e=gce(); e.children.foreground = -1; c=c+1; k=k+n+1; end // Here we have a loop in the green part because each vertex on this level curve is equal to 1. // To be clearer, let us change the color_map f.color_map = jetcolormap(1024);
See also
- contour2di — calcule les courbes de niveau d'une surface
- contour2d — level curves of a surface on a 2D plot
- contour — level curves on a 3D surface
- fec — dessin en pseudo-couleurs d'une surface définie sur un maillage constitué de polygones convexes
- plot2d — 2D plot
History
| Version | Description |
| 5.5.2 | Function contour2dm introduced. |
| Report an issue | ||
| << contour2di | 2d_plot | contourf >> |