Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
mucomp
mu (structured singular value) calculation
Syntax
[BOUND, D, G] = mucomp(Z, K, T)
Arguments
- Z
the complex n-by-n matrix for which the structured singular value is to be computed
- K
the vector of length m containing the block dimensions of the structured uncertainty
 . The uncertainty
. The uncertainty
 is supposed to be a block
diagonal matrix.
is supposed to be a block
diagonal matrix.- T
the vector of length m indicating the type of each uncertainty block. T(I) = 1 if the corresponding block is real T(I) = 2 if the corresponding block is complex.
- BOUND
the upper bound on the structured singular value.
- D, G
vectors of length n containing the diagonal entries of the diagonal matrices D and G, respectively, such that the matrix
Z'*diag(D)^2*Z + sqrt(-1)*(diag(G)*Z-Z'*diag(G)) - bound^2*diag(D)^2is negative semidefinite.
Description
This function computes an upper bound on the structured singular value for a given square complex matrix and given block structure of the uncertainty.
The structured singular value 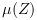 is
defined as the inverse of the norm of the smallest
uncertainty
is
defined as the inverse of the norm of the smallest
uncertainty  that makes
that makes
 . Here
. Here  is supposed to be a block diagonal matrix.
is supposed to be a block diagonal matrix.
Examples
K=[1,1,2,1,1]; T=[1,1,2,2,2]; Z=[-1+%i*6, 2-%i*3, 3+%i*8, 3+%i*8,-5-%i*9,-6+%i*2; 4+%i*2,-2+%i*5,-6-%i*7,-4+%i*11,8-%i*7, 12-%i; 5-%i*4,-4-%i*8, 1-%i*3,-6+%i*14,2-%i*5, 4+%i*16; -1+%i*6, 2-%i*3, 3+%i*8, 3+%i*8,-5-%i*9,-6+%i*2; 4+%i*2,-2+%i*5,-6-%i*7,-4+%i*11,8-%i*7, 12-%i; 5-%i*4,-4-%i*8, 1-%i*3,-6+%i*14,2-%i*5, 4+%i*16]; [BOUND, D, G] = mucomp(Z, K, T) spec(Z'*(diag(D)^2)*Z + %i*(diag(G)*Z-Z'*diag(G)) - BOUND^2*diag(D)^2)
Used functions
This function is based on the Slicot routine AB13MD.
References
Fan, M.K.H., Tits, A.L., and Doyle, J.C. Robustness in the presence of mixed parametric uncertainty and unmodeled dynamics. IEEE Trans. Automatic Control, vol. AC-36, 1991, pp. 25-38. Slicot routine AB13MD.
| Report an issue | ||
| << linmeq | Matrix Computation | ric_desc >> |