Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
lattn
recursive solution of normal equations
Syntax
[la,lb]=lattn(n,p,cov)
Arguments
- n
maximum order of the filter
- p
fixed dimension of the MA part. If
p= -1, the algorithm reduces to the classical Levinson recursions.- cov
matrix containing the
Rk's (d*dmatrices for a d-dimensional process).It must be given the following way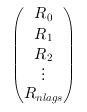
- la
list-type variable, giving the successively calculated polynomials (degree 1 to degree n),with coefficients Ak
Description
solves recursively on n (p being fixed)
the following system (normal equations), i.e. identifies
the AR part (poles) of a vector ARMA(n,p) process,
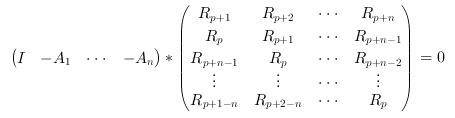
where {Rk;k=1,nlag} is the sequence of empirical covariances.
Example
//Generate the process t1=0:0.1:100; y1=sin(2*%pi*t1)+sin(2*%pi*2*t1); y1=y1+rand(y1,"normal"); //Covariance of y1 nlag=128; c1=corr(y1,nlag); c1=c1'; //Compute the filter with maximum order=15 and p=1 n=15; [la1,sig1]=lattn(n,1,c1); //Compare result of poles with p=-1 and with levin function [la2,sig2]=lattn(n,-1,c1); for i=1:n s2=roots(la2(i)); s2=log(s2)/2/%pi/.1; //estimated poles s2=gsort(imag(s2)); s2=s2(1:i/2); end; [la3,sig3]=levin(n,c1); for i=1:n s3=roots(la3(i)); s3=log(s3)/2/%pi/.1; //estimated poles s3=gsort(imag(s3)); s3=s3(1:i/2); end;
See also
| Report an issue | ||
| << frfit | Identification | lattp >> |