Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
Crank-Nicolson 2(3)
Crank-Nicolson is a numerical solver based on the Runge-Kutta scheme providing an efficient and stable implicit method to solve Ordinary Differential Equations (ODEs) Initial Value Problems. Called by xcos.
Description
Crank-Nicolson is a numerical solver based on the Runge-Kutta scheme providing an efficient and stable fixed-size step method to solve Initial Value Problems of the form:
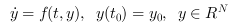
CVode and IDA use variable-size steps for the integration.
This makes the computation times unpredictable. Runge-Kutta-based solvers do not adapt to the complexity of the problem, but guarantee a stable computation time.
This method being implicit, it can be used on stiff problems.
It is an enhancement of the backward Euler method, which approximates yn+1 by computing f(tn+h, yn+1) and truncating the Taylor expansion.
By convention, to use fixed-size steps, the program first computes a fitting h that approaches the simulation parameter max step size.
An important difference of Crank-Nicolson with the previous methods is that it computes up to the second derivative of y, while the others mainly use linear combinations of y and y'.
Here, the next value is determined by the present value yn plus the weighted average of two increments, where each increment is the product of the size of the interval, h, and an estimated slope specified by the function f(t,y).
- k1 is the increment based on the slope at the midpoint of the interval, using yn + a11*h*k1/2 + a12*h*k2/2 ,
- k2 is the increment based on the slope at the midpoint of the interval, but now using yn .
We see that the computation of ki requires ki, thus necessitating the use of a nonlinear solver (here, fixed-point iterations).
First, we set k0 = h * f(tn, yn) as first guess for both ki, to get updated ki and a first value for yn+1 .
Next, we save and recompute yn+1 with those new ki.
Then, we compare the two yn+1 and recompute it until its difference with the last computed one is inferior to the simulation parameter reltol.
This process adds a significant computation time to the method, but greatly improves stability.
While computing a new k2 only requires one call to the derivative of yn ,thus making an error in O(h2) , k1 requires two calls (one for its initial computation and one for the new one). So in k1, we are approximating y(2)n , thus making an error in O(h3) .
So the total error is number of steps * O(h3) . And since number of steps = interval size / h by definition, the total error is in O(h2) .
That error analysis baptized the method Crank-Nicolson 2(3): O(h3) per step, O(h2) in total.
Although the solver works fine for max step size up to 10-3 , rounding errors sometimes come into play as we approach 4*10-4 . Indeed, the interval splitting cannot be done properly and we get capricious results.
Examples
The integral block returns its continuous state, we can evaluate it with Crank-Nicolson by running the example:
// Import the diagram and set the ending time loadScicos(); loadXcosLibs(); importXcosDiagram("SCI/modules/xcos/examples/solvers/ODE_Example.zcos"); scs_m.props.tf = 5000; // Select the solver Crank-Nicolson and set the precision scs_m.props.tol(2) = 10^-10; scs_m.props.tol(6) = 8; scs_m.props.tol(7) = 10^-2; // Start the timer, launch the simulation and display time tic(); try xcos_simulate(scs_m, 4); catch disp(lasterror()); end t = toc(); disp(t, "Time for Crank-Nicolson:");
The Scilab console displays:
Time for Crank-Nicolson:
8.911
Now, in the following script, we compare the time difference between Crank-Nicolson and CVode by running the example with the five solvers in turn: Open the script
Time for BDF / Newton:
18.894
Time for BDF / Functional:
18.382
Time for Adams / Newton:
10.368
Time for Adams / Functional:
9.815
Time for Crank-Nicolson:
6.652
These results show that on a nonstiff problem, for relatively same precision required and forcing the same step size, Crank-Nicolson competes with Adams / Functional.
Variable-size step ODE solvers are not appropriate for deterministic real-time applications because the computational overhead of taking a time step varies over the course of an application.
See also
- LSodar — LSodar (short for Livermore Solver for Ordinary Differential equations, with Automatic method switching for stiff and nonstiff problems, and with Root-finding) is a numerical solver providing an efficient and stable method to solve Ordinary Differential Equations (ODEs) Initial Value Problems.
- CVode — CVode (short for C-language Variable-coefficients ODE solver) is a numerical solver providing an efficient and stable method to solve Ordinary Differential Equations (ODEs) Initial Value Problems. It uses either BDF or Adams as implicit integration method, and Newton or Functional iterations.
- IDA — IDA (short for Implicit Differential Algebraic equations system solver) is a numerical solver providing an efficient and stable method to solve Differential Algebraic Equations system (DAEs) Initial Value Problems.
- Runge-Kutta 4(5) — Runge-Kutta is a numerical solver providing an efficient explicit method to solve Ordinary Differential Equations (ODEs) Initial Value Problems.
- Dormand-Prince 4(5) — Dormand-Prince is a numerical solver providing an efficient explicit method to solve Ordinary Differential Equations (ODEs) Initial Value Problems.
- Implicit Runge-Kutta 4(5) — Implicit Runge-Kutta is a numerical solver providing an efficient and stable implicit method to solve Ordinary Differential Equations (ODEs) Initial Value Problems. Called by xcos.
- DDaskr — DDaskr (short for Double-precision Differential Algebraic equations system Solver with Krylov method and Rootfinding) is a numerical solver providing an efficient and stable method to solve Differential Algebraic Equations systems (DAEs) Initial Value Problems.
- Comparisons — This page compares solvers to determine which one is best fitted for the studied problem.
- ode_discrete — 常微分方程式ソルバ, 離散時間シミュレーション
- ode_root — 求解付きの常微分方程式ソルバ
- odedc — 離散/連続 ODE ソルバ
- impl — 微分代数方程式
Bibliography
Advances in Computational Mathematics, Volume 6, Issue 1, 1996, Pages 207-226 A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type
Pages 81-82 A family of higher-order implicit time integration methods for unsteady compressible flows
History
| Version | Description |
| 6.0.0 | Crank-Nicolson 2(3) solver added |
| Report an issue | ||
| << Implicit Runge-Kutta 4(5) | Solvers | IDA >> |