Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
qp_solve
linear quadratic programming solver builtin
Syntax
[x [,iact [,iter [,f [,info]]]]] = qp_solve(Q, p, C, b, me)
Arguments
- Q
real positive definite symmetric matrix (dimension
n x n).- p
real (column) vector (dimension
n)- C
real matrix (dimension
(me + md) x n). This matrix may be dense or sparse.- b
RHS column vector (dimension
m=(me + md))- me
number of equality constraints (i.e.
x'*C(:,1:me) = b(1:me)')- x
optimal solution found.
- iact
vector, indicator of active constraints. The non zero entries give the index of the active constraints. The entries of the iact vector are ordered this way: equality constraints come first, then come the inequality constraints.
- iter
2x1 vector, first component gives the number of "main" iterations, the second one says how many constraints were deleted after they became active.
- info
integer, error flag. If it is present and qp_solve encounters an error, then a warning is issued. The current results are returned, so in this case they are probably inaccurate.
Description
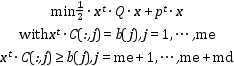
This function requires Q to be symmetric positive
definite. If this hypothesis is not satisfied, one may use the contributed
quapro toolbox.
Examples
// Find x in R^6 such that: // x'*C1 = b1 (3 equality constraints i.e me=3) C1= [ 1,-1, 2; -1, 0, 5; 1,-3, 3; 0,-4, 0; 3, 5, 1; 1, 6, 0]; b1=[1;2;3]; // x'*C2 >= b2 (2 inequality constraints i.e md=2) C2= [ 0 ,1; -1, 0; 0,-2; -1,-1; -2,-1; 1, 0]; b2=[ 1;-2.5]; // and minimize 0.5*x'*Q*x - p'*x with p=[-1;-2;-3;-4;-5;-6]; Q=eye(6,6); me=3; [x,iact,iter,f]=qp_solve(Q,p,[C1 C2],[b1;b2],me) // Only linear constraints (1 to 4) are active
See also
The contributed toolbox "quapro" may also be of interest, in
particular for singular Q.
Memory requirements
Let r be
r=min(m,n)
Then the memory required by qp_solve during the computations is
2*n+r*(r+5)/2 + 2*m +1
References
Goldfarb, D. and Idnani, A. (1982). "Dual and Primal-Dual Methods for Solving Strictly Convex Quadratic Programs", in J.P. Hennart (ed.), Numerical Analysis, Proceedings, Cocoyoc, Mexico 1981, Vol. 909 of Lecture Notes in Mathematics, Springer-Verlag, Berlin, pp. 226-239.
Goldfarb, D. and Idnani, A. (1983). "A numerically stable dual method for solving strictly convex quadratic programs", Mathematical Programming 27: 1-33.
QuadProg (Quadratic Programming Routines), Berwin A Turlach,http://www.maths.uwa.edu.au/~berwin/software/quadprog.html
Used Functions
qpgen2.f and >qpgen1.f (also named QP.solve.f) developed by Berwin A. Turlach according to the Goldfarb/Idnani algorithm
History
| Version | Description |
| 5.5.0 | Fifth output argument info added for error information. |
| Report an issue | ||
| << qld | Optimization and Simulation | qpsolve >> |