Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
interp1
one_dimension interpolation function
Syntax
[yp]=interp1(x, y,xp [, method,[extrapolation]])
Arguments
- xp
reals scalar, vector or matrix (or hypermatrix)
- x
reals vector
- method
(optional) string defining the interpolation method
- extrapolation
(optional) string, or real value defining the yp(j) components for xp(j) values outside [x1,xn] interval.
- yp
vector, or matrix (or hypermatrix)
Description
Given (x,y,xp), this function performs the yp
components corresponding to xp by the interpolation(linear by default)
defined by x and y.
If yp is a vector then the length of xp is equal
to the length of yp, if yp is a
matrix then xp have the same length than the length of
each columns of yp, if yp is a hypermatrix then the
length of xp have the same length than the first
dimension of yp.
If size(y)=[C,M1,M2,M3,...,Mj] and size(xp)=[N1,N2,N3,...,Nk] then size(yp)=[N1,N2,..,Nk,M1,M2,...Mj] and length of x must be equal to size(y,1)
The method parameter sets the evaluation rule for
interpolation
- "linear"
the interpolation is defined by linear method (see interpln)
- "spline"
the interpolation is defined by cubic spline interpolation ( see splin , interp)
- "nearest"
for each value xp(j), yp(j) takes the value or y(i) corresponding to x(i) the nearest neighbor of xp(j)
The extrapolation parameter sets the evaluation
rule for extrapolation, i.e for xp(i)not in [x1,xn]
interval
- "extrap"
the extrapolation is performed by the defined method. yp=interp1(x,y,xp,method,"extrap")
- real value
you can choose a real value for extrapolation, in this way yp(i) takes this value for xp(i) not in [x1,xn] interval, for example 0 (but also nan or inf). yi=interp1(x,y,xp,method, 0)
- by default
the extrapolation is performed by the defined method (for spline method), and by nan for linear and nearest methods. yp=interp1(x,y,xp,method)
Examples
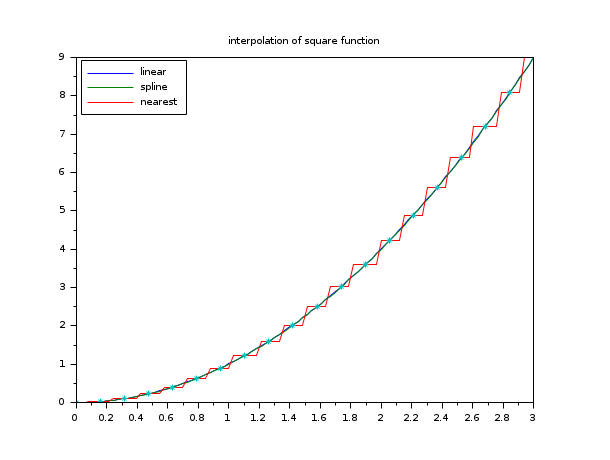
x=linspace(0,3,20); y=x.^2; xx=linspace(0,3,100); yy1=interp1(x,y,xx,'linear'); yy2=interp1(x,y,xx,'spline'); yy3=interp1(x,y,xx,'nearest'); plot(xx',[yy1;yy2;yy3]',x,y,'*') xtitle('interpolation of square function') legend(['linear','spline','nearest'],a=2)
See also
History
| Версия | Описание |
| 5.4.0 | previously, imaginary part of input arguments were implicitly ignored. |
| Report an issue | ||
| << interp | Interpolation | interp2d >> |