Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
armax
armax identification
Syntax
[arc,la,lb,sig,resid]=armax(r,s,y,u,[b0f,prf])
Arguments
- y
output process y(ny,n); ( ny: dimension of y , n : sample size)
- u
input process u(nu,n); ( nu: dimension of u , n : sample size)
- r and s
auto-regression orders r >=0 et s >=-1
- b0f
optional parameter. Its default value is 0 and it means that the coefficient b0 must be identified. if bof=1 the b0 is supposed to be zero and is not identified
- prf
optional parameter for display control. If prf =1, the default value, a display of the identified Arma is given.
- arc
a Scilab arma object (see armac)
- la
is the list(a,a+eta,a-eta) ( la = a in dimension 1) ; where eta is the estimated standard deviation. , a=[Id,a1,a2,...,ar] where each ai is a matrix of size (ny,ny)
- lb
is the list(b,b+etb,b-etb) (lb =b in dimension 1) ; where etb is the estimated standard deviation. b=[b0,.....,b_s] where each bi is a matrix of size (nu,nu)
- sig
is the estimated standard deviation of the noise and resid=[ sig*e(t0),....] (
Description
armax is used to identify the coefficients of a n-dimensional ARX process
A(z^-1)y= B(z^-1)u + sig*e(t)
where e(t) is a n-dimensional white noise with variance I. sig an nxn matrix and A(z) and B(z):
A(z) = 1+a1*z+...+a_r*z^r; ( r=0 => A(z)=1) B(z) = b0+b1*z+...+b_s z^s ( s=-1 => B(z)=0)
for the method see Eykhoff in trends and progress in system identification, page 96.
with
z(t)=[y(t-1),..,y(t-r),u(t),...,u(t-s)]
and
coef= [-a1,..,-ar,b0,...,b_s]
we can write
y(t)= coef* z(t) + sig*e(t) and the algorithm minimises
sum_{t=1}^N ( [y(t)- coef'z(t)]^2)
where t0=max(max(r,s)+1,1))).
Examples
//-Ex1- Arma model : y(t) = 0.2*u(t-1)+0.01*e(t-1) ny=1,nu=1,sig=0.01; Arma=armac(1,[0,0.2],[0,1],ny,nu,sig) //defining the above arma model u=rand(1,1000,'normal'); //a random input sequence u y=arsimul(Arma,u); //simulation of a y output sequence associated with u. Armaest=armax(0,1,y,u); //Identified model given u and y. Acoeff=Armaest('a'); //Coefficients of the polynomial A(x) Bcoeff=Armaest('b') //Coefficients of the polynomial B(x) Dcoeff=Armaest('d'); //Coefficients of the polynomial D(x) [Ax,Bx,Dx]=arma2p(Armaest) //Results in polynomial form.
//-Ex2- Arma1: y_t -0.8*y_{t-1} + 0.2*y_{t-2} = sig*e(t) ny=1,nu=1;sig=0.001; // First step: simulation the Arma1 model, for that we define // Arma2: y_t -0.8*y_{t-1} + 0.2*y_{t-2} = sig*u(t) // with normal deviates for u(t). Arma2=armac([1,-0.8,0.2],sig,0,ny,nu,0); //Definition of the Arma2 arma model (a model with B=sig and without noise!) u=rand(1,10000,'normal'); // An input sequence for Arma2 y=arsimul(Arma2,u); // y = output of Arma2 with input u // can be seen as output of Arma1. // Second step: identification. We look for an Arma model // y(t) + a1*y(t-1) + a2 *y(t-2) = sig*e(t) Arma1est=armax(2,-1,y,[]); [A,B,D]=arma2p(Arma1est)
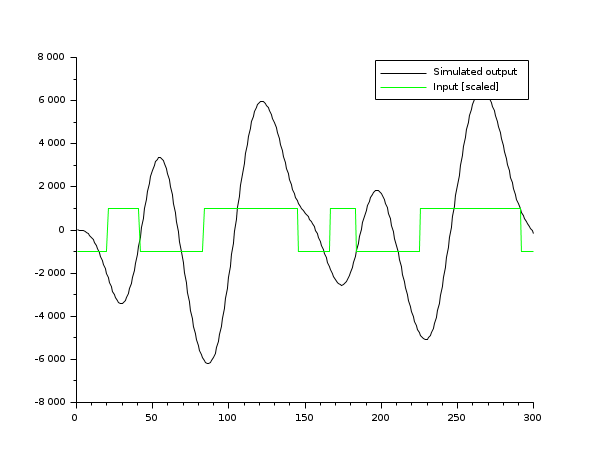
a = [1, -2.851, 2.717, -0.865]; b = [0, 1, 1, 1]; d = [1, 0.7, 0.2]; ar = armac(a, b, d, 1, 1, 1); disp(_("Simulation of an ARMAX process:")); disp(ar); // The input n = 300; u = -prbs_a(n, 1, int([2.5,5,10,17.5,20,22,27,35]*100/12)); // simulation zd = narsimul(ar, u); // visualization plot2d(1:n,[zd',1000*u'],style=[1,3]);curves = gce(); legend(["Simulated output";"Input [scaled]"])
See also
| Report an issue | ||
| << arl2 | Identification | armax1 >> |