Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
intg
definite integral
Syntax
[v, err [,ierr]]=intg(a, b, f [,ea [,er]])
Arguments
- a, b
real numbers.
- f
external (function or list or string).
- ea, er
real numbers.
- ea
absolute error required on the result. Default value: 1.d-14.
- er
relative error required on the result. Default value: 1.d-8.
- err
estimated absolute error on the result.
- ierr
error flag number (= 0 if no error occurred).
Description
intg(a,b,f) evaluates the definite integral from
a to b of f(t)dt.
The function f(t) should be continuous.
The evaluation hopefully satisfies following claim for accuracy:
abs(I-v)<= max(ea,er*abs(I)) where
I stands for the exact value of the integral.
f is an external :
If f is function its definition must be as
follows y = f(t)
If f is a list the list must be as follows:
list(f,x1,x2,...) where f is a
function with syntax f(t,x1,x2,...).
If f is a string it refers to the name of a
Fortran function or a C procedure with a given syntax:
In the fortran case the calling sequence should be double
precision function f(x)
where x is also a
double precision number.
In the C case the syntax should be double
f(double *x)
.
Known Limitation
Like all the integrators, intg is subject to spike missing.
A flat function with a spike will be seen as a fully flat function if the spike is stiff enough.
This cannot be bypassed, it is easy to understand why when we know how the integrator operates.
Indeed, intg uses the 21-point Gauss-Kronrod rule,
so if there is a spike in-between two consecutive integration points,
then it will go undetected, the function will be considered smooth.
However, a warning message will be issued if the function is considered very smooth. The user will then be suggested to reduce the integration interval, should he think that spikes were missed.
The following graphs illustrate that phenomenon.
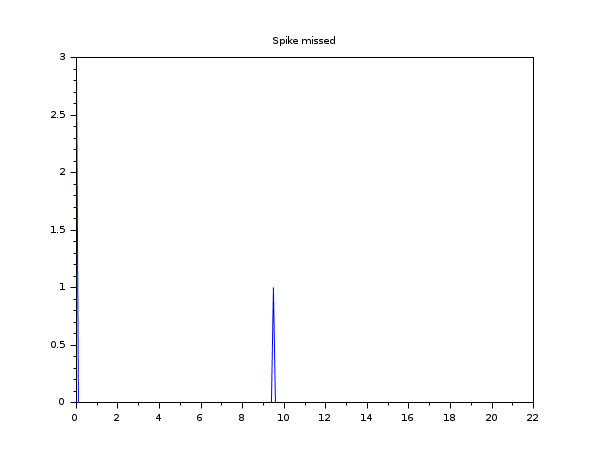
Being in-between the 9th and 10th integration points,
that spike is not detected and
intg considers the function flat.
In the next image, the spike is large enough to be covered by the integration points.
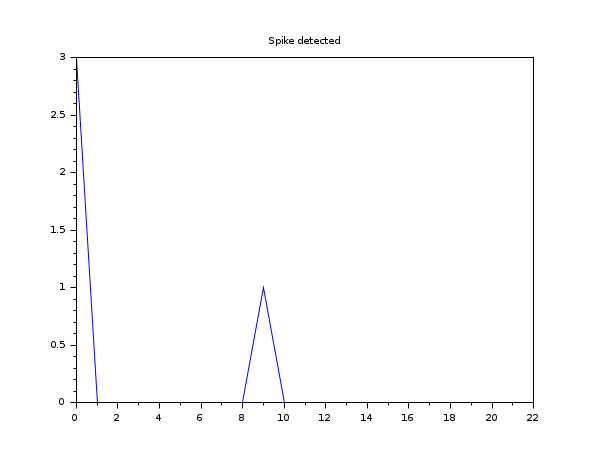
If the user wants to display the computed solution even if the solver has encountered an error,
he should add the third output argument ierr, that will transform the
errors into warnings. This is mostly used in the case of rounding errors.
Examples
// Function written in the Scilab language function y=f(x),y=x*sin(30*x)/sqrt(1-((x/(2*%pi))^2)),endfunction exact=-2.5432596188; I=intg(0,2*%pi,f) abs(exact-I) // Function with an argument written in the Scilab language function y=f1(x, w),y=x*sin(w*x)/sqrt(1-((x/(2*%pi))^2)),endfunction I=intg(0,2*%pi,list(f1,30)) abs(exact-I) // Function written in Fortran (a Fortran compiler is required) // define a Fortran function cd TMPDIR; F=[' double precision function ffun(x)' ' double precision x,pi' ' pi=3.14159265358979312d+0' ' ffun=x*sin(30.0d+0*x)/sqrt(1.0d+0-(x/(2.0d+0*pi))**2)' ' return' ' end']; mputl(F,fullfile(TMPDIR,'ffun.f')) // compile the function l=ilib_for_link('ffun',fullfile(TMPDIR,'ffun.f'),[],'f'); // add the function to the working environment link(l,'ffun','f') // integrate the function I=intg(0,2*%pi,'ffun') abs(exact-I) // Function written in C (a C compiler is required) // define a C function C=['#include <math.h>' 'double cfun(double *x)' '{' ' double y,pi=3.14159265358979312;' ' y=*x/(2.0e0*pi);' ' return *x*sin(30.0e0**x)/sqrt(1.0e0-y*y);' '}']; mputl(C,fullfile(TMPDIR,'cfun.c')) // compile the function l=ilib_for_link('cfun',fullfile(TMPDIR,'cfun.c'),[],'c'); // add the function to the working environment link(l,'cfun','c') // integrate the function I=intg(0,2*%pi,'cfun') abs(exact-I)
See also
Used Functions
The associated routines can be found in SCI/modules/differential_equations/src/fortran directory :
dqags.f and dqagse.f from quadpack
| Report an issue | ||
| << integrate | Differential calculus, Integration | intl >> |