Scilab 5.5.2
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
hank
共分散からハンケル行列を得る
呼び出し手順
hk =hank(m, n, cov)
引数
- m
ブロック行の数
- n
ブロック列の数
- cov
共分散の系列; 次のように指定します :[R0 R1 R2...Rk]
- hk
ハンケル行列の計算値
説明
この関数は,ベクトル過程の共分散系列から
大きさ(m*d,n*d)のハンケル行列を構築します.
より正確には以下となります:
この関数は,ベクトル過程の共分散系列から
大きさ(m*d,n*d)のハンケル行列を作成します.
より正しくは:
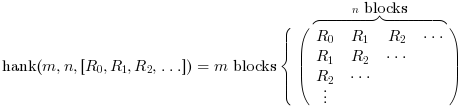
例
//Example of how to use the hank macro for //building a Hankel matrix from multidimensional //data (covariance or Markov parameters e.g.) // //This is used e.g. in the solution of normal equations //by classical identification methods (Instrumental Variables e.g.) // //1)let's generate the multidimensional data under the form : // C=[c_0 c_1 c_2 .... c_n] //where each bloc c_k is a d-dimensional matrix (e.g. the k-th correlation //of a d-dimensional stochastic process X(t) [c_k = E(X(t) X'(t+k)], ' //being the transposition in scilab) // //we take here d=2 and n=64 c = rand(2, 2 * 64) //generate the hankel matrix H (with 4 bloc-rows and 5 bloc-columns) //from the data in c H = hank(4, 5, c);
参照
- toeplitz — toeplitz行列
| Report an issue | ||
| << fft | transforms | hilb >> |