Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
histc
computes an histogram
Calling Sequence
[cf, ind] = histc(n, data [,normalization]) [cf, ind] = histc(x, data [,normalization])
Arguments
- n
positive integer (number of classes)
- x
increasing vector defining the classes (
xmay have at least 2 components)- data
vector (data to be analysed)
- cf
vector representing the number of values of
datafalling in the classes defined bynorx- ind
vector or matrix of same size as
data, representing the repective belonging of each element of datadatato the classes defined bynorx- normalization
scalar boolean.
normalization=%f (default):cfrepresents the total number of points in each class,normalization=%t:cfrepresents the number of points in each class, relatively to the total number of points
Description
This function computes a histogram of the data vector using the
classes x. When the number n of classes is provided
instead of x, the classes are chosen equally spaced and
x(1) = min(data) < x(2) = x(1) + dx < ... < x(n+1) = max(data)
with dx = (x(n+1)-x(1))/n.
The classes are defined by C1 = [x(1), x(2)] and Ci = ( x(i), x(i+1)] for i >= 2.
Noting Nmax the total number of data (Nmax = length(data))
and Ni the number of data components falling in
Ci, the value of the histogram for x in
Ci is equal to Ni/(Nmax (x(i+1)-x(i))) when
"normalized" is selected and else, simply equal to Ni.
When normalization occurs the histogram verifies:
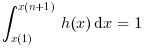
when x(1)<=min(data) and max(data) <= x(n+1)
Examples
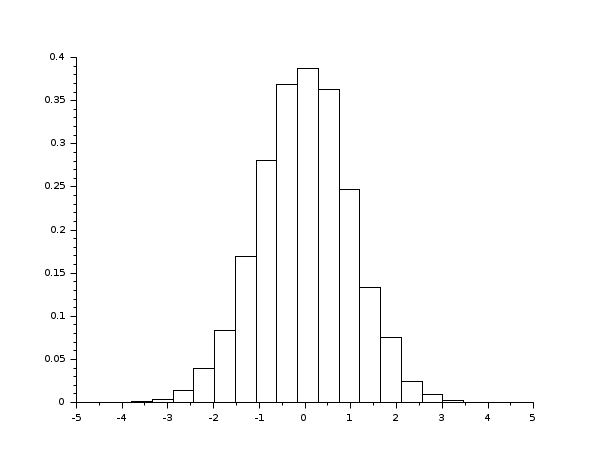
- Example #1: variations around a histogram of a gaussian random sample
// The gaussian random sample d = rand(1, 10000, 'normal'); [cf, ind] = histc(20, d, normalization=%f) // We use histplot to show a graphic representation clf(); histplot(20, d, normalization=%f); [cf, ind] = histc(20, d) clf(); histplot(20, d);
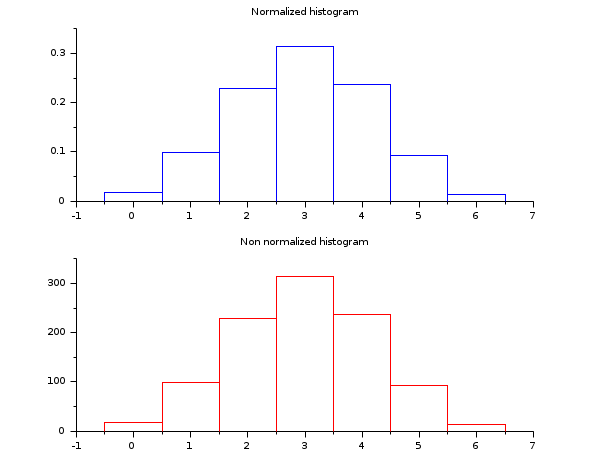
- Example #2: histogram of a binomial (B(6,0.5)) random sample
d = grand(1000,1,"bin", 6, 0.5); c = linspace(-0.5,6.5,8); clf() subplot(2,1,1) [cf, ind] = histc(c, d) histplot(c, d, style=2); xtitle("Normalized histogram") subplot(2,1,2) [cf, ind] = histc(c, d, normalization=%f) histplot(c, d, normalization=%f, style=5); xtitle("Non normalized histogram")
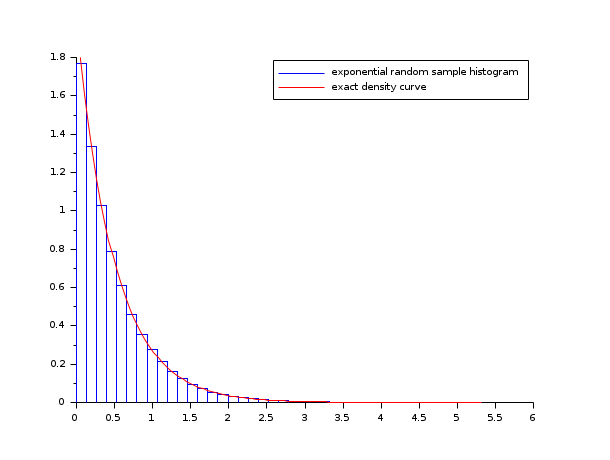
- Example #3: histogram of an exponential random sample
lambda = 2; X = grand(100000,1,"exp", 1/lambda); Xmax = max(X); [cf, ind] = histc(40, X) clf() histplot(40, X, style=2); x = linspace(0, max(Xmax), 100)'; plot2d(x, lambda*exp(-lambda*x), strf="000", style=5) legend(["exponential random sample histogram" "exact density curve"]);
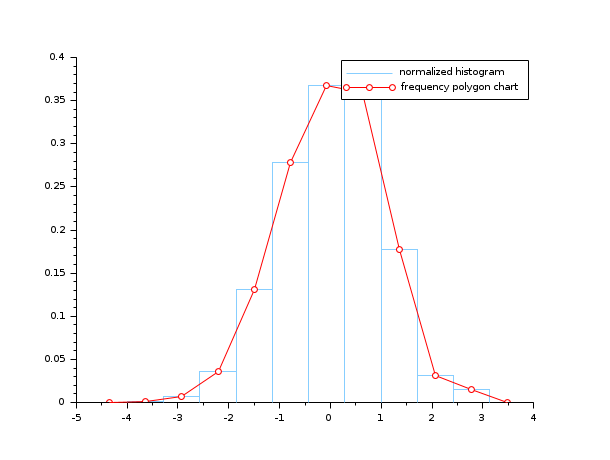
- Example #4: the frequency polygon chart and the histogram of a gaussian random sample
n = 10; data = rand(1, 1000, "normal"); [cf, ind] = histc(n, data) clf(); histplot(n, data, style=12, polygon=%t); legend(["normalized histogram" "frequency polygon chart"]);
See Also
History
| Version | Description |
| 5.5.0 | Introduction |
| Report an issue | ||
| << covar | Descriptive Statistics | median >> |