- Справка Scilab
- Signal Processing
- filters
- analpf
- buttmag
- casc
- cheb1mag
- cheb2mag
- convol
- ell1mag
- eqfir
- eqiir
- faurre
- ffilt
- filter
- find_freq
- frmag
- fsfirlin
- group
- iir
- iirgroup
- iirlp
- kalm
- lev
- levin
- lindquist
- remez
- remezb
- srfaur
- srkf
- sskf
- syredi
- system
- trans
- wfir
- wiener
- wigner
- window
- yulewalk
- zpbutt
- zpch1
- zpch2
- zpell
Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
group
group delay for digital filter
Calling Sequence
[tg [,fr]] = group(npts, H) (call with a siso transfert function) [tg [,fr]] = group(npts, C) (call with a vector of transfert functions, cascaded second order representation) [tg [,fr]] = group(npts, F) (call with the vector of an FIR filter coefficients) [tg [,fr]] = group(npts, a1i, a2i, b1i, b2i) (call with 4 vectors of numbers, cascaded second order Deczky representation)
Arguments
- npts
integer : number of points desired in calculation of group delay
- a1i
in coefficient, polynomial, rational polynomial, or cascade polynomial form this variable is the transfer function of the filter. In coefficient polynomial form this is a vector of coefficients (see below).
- a2i
in coeff poly form this is a vector of coeffs
- b1i
in coeff poly form this is a vector of coeffs
- b2i
in coeff poly form this is a vector of coeffs
- tg
values of group delay evaluated on the grid fr
- fr
grid of normalized frequency values where group delay is evaluated
Description
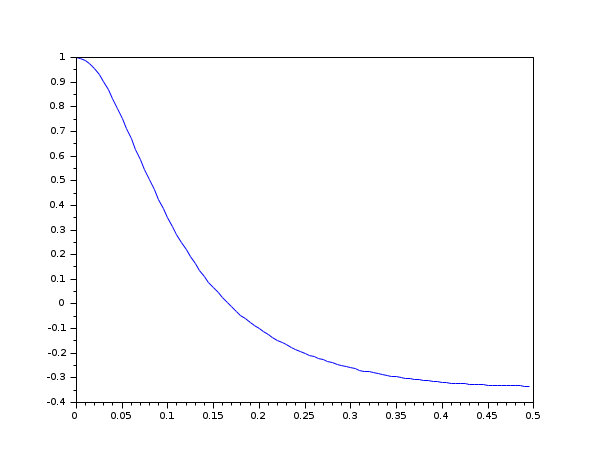
Calculate the group delay of a digital filter with transfer function h(z).
The filter specification can be in coefficient form, polynomial form, rational polynomial form, cascade polynomial form, or in coefficient polynomial form.
In the coefficient polynomial form the transfer function is formulated by the following expression
h(z)=prod(a1i+a2i*z+z**2)/prod(b1i+b2i*z+z^2)
Examples
s = poly(0, "s"); h_cont = syslin("c", 1/(s-10)); h = ss2tf(cls2dls(tf2ss(h_cont), 0.1)); [tg, fr] = group(100, h); plot(fr, tg)
| Report an issue | ||
| << fsfirlin | filters | iir >> |