Sfgrayplot

Аргументы

x, y

вещественные векторы-строки размером n1 и n2.

f

Scilab-функция (z=f(x,y)).

<opt_args>

представляет последовательность инструкций key1=value1, key2=value2, ..., где key1, key2, ... может быть одним из следующих: strf, rect, nax, zminmax, colminmax, mesh, colout (о первых трёх см. plot2d, а о последних четырёх см. fec).

strf, rect, nax

см. plot2d.

zminmax, colminmax, mesh, colout

см. fec.

Описание

Функция Sfgrayplot - это то же самое, что и fgrayplot, но график сглажен. Для сглаживания используется функция fec. Поверхность строится в предположении, что она линейна на множестве треугольников, построенных из сетки (здесь с n1=5, n2=3):

 
_____________
| /| /| /| /|
|/_|/_|/_|/_| 
| /| /| /| /| 
|/_|/_|/_|/_|
 

Чтобы увидеть цветовую шкалу, может быть использована функция colorbar (но вы должны знать (или вычислить) минимальное и максимальное значения).

Вместо функции Sfgrayplot, вы можете использовать функцию Sgrayplot, и это может быть несколько быстрее.

Введите команду Sfgrayplot(), чтобы посмотреть наглядную иллюстрацию.

Примеры

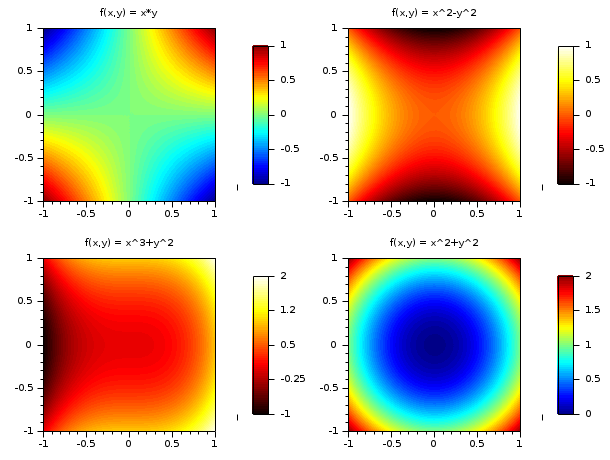
// Пример №1: построение 4 поверхностей
function z=surf1(x, y), z=x*y, endfunction
function z=surf2(x, y), z=x^2-y^2, endfunction
function z=surf3(x, y), z=x^3+y^2, endfunction
function z=surf4(x, y), z=x^2+y^2, endfunction
clf()
set(gcf(),"color_map",[jetcolormap(64);hotcolormap(64)])
x = linspace(-1,1,60);
y = linspace(-1,1,60);
drawlater() ;
subplot(2,2,1)
  colorbar(-1,1,[1,64])
  Sfgrayplot(x,y,surf1,strf="041",colminmax=[1,64])
  xtitle("f(x,y) = x*y")
subplot(2,2,2)
  colorbar(-1,1,[65,128])
  Sfgrayplot(x,y,surf2,strf="041",colminmax=[65,128])
  xtitle("f(x,y) = x^2-y^2")
subplot(2,2,3)
  colorbar(-1,2,[65,128])
  Sfgrayplot(x,y,surf3,strf="041",colminmax=[65,128])
  xtitle("f(x,y) = x^3+y^2")
subplot(2,2,4)
  colorbar(0,2,[1,64])
  Sfgrayplot(x,y,surf4,strf="041",colminmax=[1,64])
  xtitle("f(x,y) = x^2+y^2")
drawnow() ;
show_window()

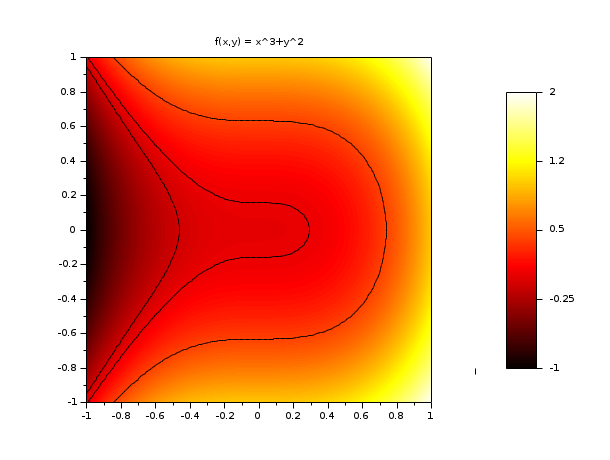
// Пример №2: построение surf3 и добавление некоторых контурных линий
function z=surf3(x, y), z=x^3+y^2, endfunction
clf()
x = linspace(-1,1,60);
y = linspace(-1,1,60);
set(gcf(),"color_map",hotcolormap(128))
drawlater() ;
colorbar(-1,2)
Sfgrayplot(x,y,surf3,strf="041")
contour2d(x,y,surf3,[-0.1, 0.025, 0.4],style=[1 1 1],strf="000")
xtitle("f(x,y) = x^3+y^2")
drawnow() ;
show_window()

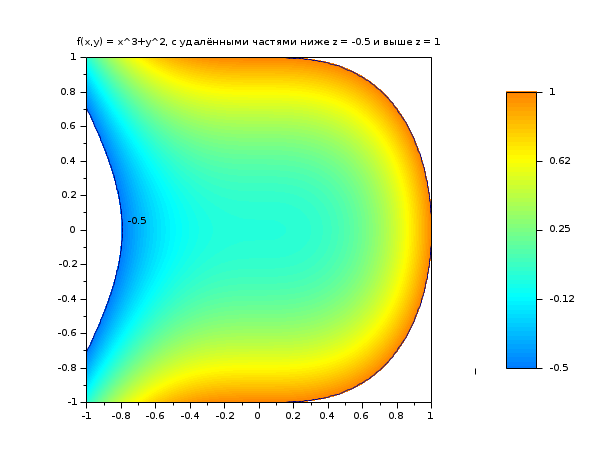
// Пример №3: построение surf3 и использование необязательных аргументов
//            zminmax и colout для ограничения графика в -0.5 <= z <= 1
function z=surf3(x, y), z=x^3+y^2, endfunction
clf()
x = linspace(-1,1,60);
y = linspace(-1,1,60);
set(gcf(),"color_map",jetcolormap(128))
drawlater() ;
zminmax = [-0.5 1]; colors=[32 96];
colorbar(zminmax(1),zminmax(2),colors)
Sfgrayplot(x, y, surf3, strf="041", zminmax=zminmax, colout=[0 0], colminmax=colors)
contour2d(x,y,surf3,[-0.5, 1],style=[1 1 1],strf="000")
xtitle("f(x,y) = x^3+y^2, с удалёнными частями ниже z = -0.5 и выше z = 1")
drawnow() ;
show_window()

Смотрите также

• fec — pseudo-color plot of a function defined on a triangular mesh
• fgrayplot — 2D plot of a surface defined by a function using colors
• grayplot — 2D plot of a surface using colors
• Sgrayplot — smooth 2D plot of a surface using colors