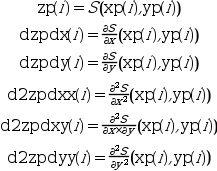eval_cshep2d

パラメータ

xp, yp

同じ大きさの実数ベクトル (または行列)

tl_coef

3次シェパード補間関数を定義する (cshep2d型の) tlist scilab 構造体 (以下では Sと呼びます)

zp

vxp および ypと同じ大きさのベクトル(または行列)で, これらの点における補間Sを評価します

dzpdx,dzpdy

xp および ypと 同じ大きさのベクトル(または行列)で, これらの点におけるSの1階微分の評価値

d2zpdxx,d2zpdxy,d2zpdyy

xp および ypと 同じ大きさのベクトル(または行列)で, これらの点におけるSの2階微分の評価値

説明

この関数は,cshep2dで計算される 3次シェパード補間関数の評価ルーチンで, 以下のようになります:

注意

補間式 S は C2 (2階連続微分可能)ですが, 十分遠い補間点(x,y)について0 により 拡張されます. これにより,補間点のかなり外側の領域に不連続が発生しますが, 実用上は問題とはなりません (一般に,補間点の外側での評価(すなわち補外)は かなり精度が劣化します).

例

// see example section of cshep2d

// this example shows the behavior far from the interpolation points ...
deff("z=f(x,y)","z = 1+ 50*(x.*(1-x).*y.*(1-y)).^2")
x = linspace(0,1,10);
[X,Y] = ndgrid(x,x);
X = X(:); Y = Y(:); Z = f(X,Y);
S = cshep2d([X Y Z]);
// evaluation inside and outside the square [0,1]x[0,1]
m = 40;
xx = linspace(-1.5,0.5,m);
[xp,yp] = ndgrid(xx,xx);
zp = eval_cshep2d(xp,yp,S);
// compute facet (to draw one color for extrapolation region
// and another one for the interpolation region)
[xf,yf,zf] = genfac3d(xx,xx,zp);
color = 2*ones(1,size(zf,2));
// indices corresponding to facet in the interpolation region
ind=find( mean(xf,"r")>0 & mean(xf,"r")<1 & mean(yf,"r")>0 & mean(yf,"r")<1 );
color(ind)=3;
clf();
plot3d(xf,yf,list(zf,color), flag=[2 6 4])
legends(["extrapolation region","interpolation region"],[2 3],1)
show_window()

参照

• cshep2d — 2次元3次シェパード(散布)補間