Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
interp2d
bicubic spline (2d) evaluation function
Calling Sequence
[zp[, dzpdx, dzpdy[, d2zpdxx, d2zpdxy, d2zpdyy]]]=interp2d(xp, yp, x, y, C [,out_mode])
Arguments
- xp
a mx-by-my matrix of doubles, the
xcoordinates of the points where the spline is to be evaluated.- yp
a mx-by-my matrix of doubles, the
ycoordinates of the points where the spline is to be evaluated.- x
a 1-by-nx matrix of doubles, the
xcoordinate of the interpolation points. We must have x(i)<x(i+1), for i=1,2,...,nx-1.- y
a 1-by-ny matrix of doubles, the
ycoordinate of the interpolation points. We must have y(i)<y(i+1), for i=1,2,...,ny-1.- C
The coefficients of the bicubic spline. The input argument of the interp2d function is the output argument of the splin2d function.
- out_mode
a 1-by-1 matrix of strings, the evaluation of s outside the range [x(1),x(nx)] by [y(1),y(ny)].
- zp
a mx-by-my matrix of doubles, the evaluation of the
zcoordinate of the spline, i.e. zp(i,j)=s(xp(i,j),yp(i,j)), for i=1,2,...,mx and j = 1,2,...,my.- dzpdx
a mx-by-my matrix of doubles, the first derivative of the spline with respect to
x.- dzpdy
a mx-by-my matrix of doubles, the first derivative of the spline with respect to
y.- d2zpdxx
a mx-by-my matrix of doubles, the second derivative of the spline with respect to
x.- d2zpdxy
a mx-by-my matrix of doubles, the second derivative of the spline with respect to
xandy.- d2zpdyy
a mx-by-my matrix of doubles, the second derivative of the spline with respect to
y.
Description
Given three vectors (x,y,C) defining a bicubic
spline or sub-spline function (see splin2d)
this function evaluates s (and ds/dx,
ds/dy, d2s/dxx, d2s/dxy, d2s/dyy
if needed) at
(xp(i),yp(i)) :
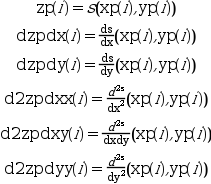
The out_mode parameter defines the evaluation
rule for extrapolation, i.e. for (xp(i),yp(i)) not in
[x(1),x(nx)]x[y(1),y(ny)]
:
- "by_zero"
an extrapolation by zero is done
- "by_nan"
extrapolation by Nan
- "C0"
the extrapolation is defined as follows :
- "natural"
the extrapolation is done by using the nearest bicubic-patch from (x,y).
- "periodic"
sis extended by periodicity.
Examples
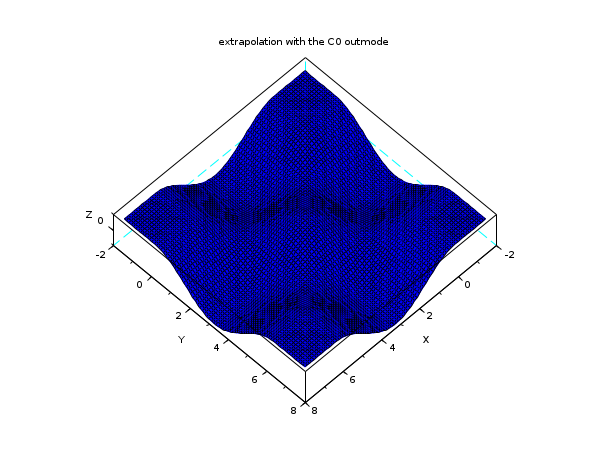
n = 7; // a n x n interpolation grid x = linspace(0,2*%pi,n); y = x; z = cos(x')*cos(y); C = splin2d(x, y, z, "periodic"); // now evaluate on a bigger domain than [0,2pi]x [0,2pi] m = 80; // discretisation parameter of the evaluation grid xx = linspace(-0.5*%pi,2.5*%pi,m); yy = xx; [XX,YY] = ndgrid(xx,yy); zz1 = interp2d(XX,YY, x, y, C, "C0"); plot3d(xx, yy, zz1, flag=[2 6 4]) xtitle("extrapolation with the C0 outmode")
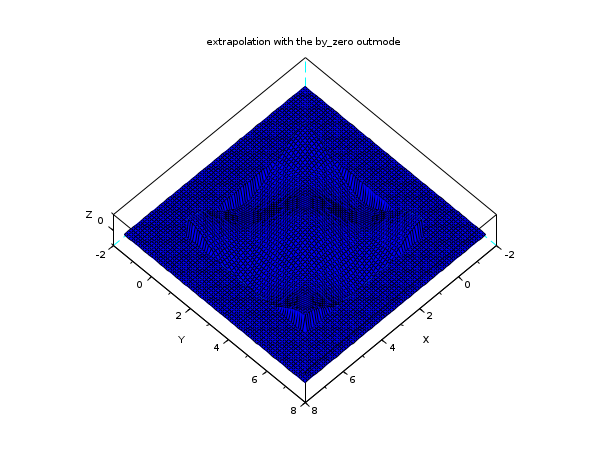
n = 7; // a n x n interpolation grid x = linspace(0,2*%pi,n); y = x; z = cos(x')*cos(y); C = splin2d(x, y, z, "periodic"); // now evaluate on a bigger domain than [0,2pi]x [0,2pi] m = 80; // discretisation parameter of the evaluation grid xx = linspace(-0.5*%pi,2.5*%pi,m); yy = xx; [XX,YY] = ndgrid(xx,yy); zz2 = interp2d(XX,YY, x, y, C, "by_zero"); plot3d(xx, yy, zz2, flag=[2 6 4]) xtitle("extrapolation with the by_zero outmode")
n = 7; // a n x n interpolation grid x = linspace(0,2*%pi,n); y = x; z = cos(x')*cos(y); C = splin2d(x, y, z, "periodic"); // now evaluate on a bigger domain than [0,2pi]x [0,2pi] m = 80; // discretisation parameter of the evaluation grid xx = linspace(-0.5*%pi,2.5*%pi,m); yy = xx; [XX,YY] = ndgrid(xx,yy); zz3 = interp2d(XX,YY, x, y, C, "periodic"); plot3d(xx, yy, zz3, flag=[2 6 4]) xtitle("extrapolation with the periodic outmode")

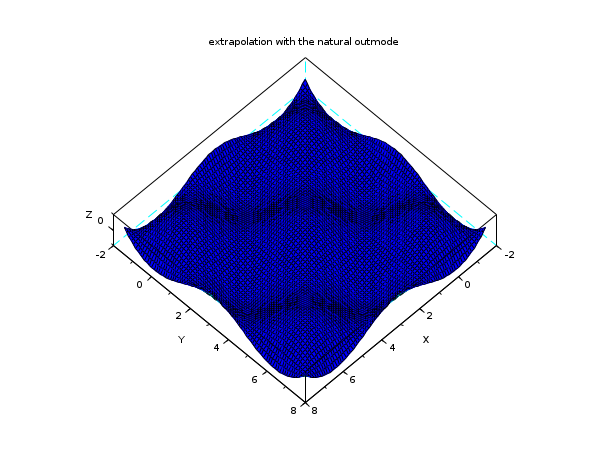
n = 7; // a n x n interpolation grid x = linspace(0,2*%pi,n); y = x; z = cos(x')*cos(y); C = splin2d(x, y, z, "periodic"); // now evaluate on a bigger domain than [0,2pi]x [0,2pi] m = 80; // discretisation parameter of the evaluation grid xx = linspace(-0.5*%pi,2.5*%pi,m); yy = xx; [XX,YY] = ndgrid(xx,yy); zz4 = interp2d(XX,YY, x, y, C, "natural"); plot3d(xx, yy, zz4, flag=[2 6 4]) xtitle("extrapolation with the natural outmode")
See Also
- splin2d — bicubic spline gridded 2d interpolation
History
| Version | Description |
| 5.4.0 | Previously, imaginary part of input arguments were implicitly ignored. |
| Report an issue | ||
| << interp1 | Interpolation | interp3d >> |