Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
interp
cubic spline evaluation function
Calling Sequence
[yp [,yp1 [,yp2 [,yp3]]]]=interp(xp, x, y, d [, out_mode])
Arguments
- xp
real vector or matrix
- x,y,d
real vectors of the same size defining a cubic spline or sub-spline function (called
sin the following)- out_mode
(optional) string defining the evaluation of
soutside the [x1,xn] interval- yp
vector or matrix of same size than
xp, elementwise evaluation ofsonxp(yp(i)=s(xp(i) or yp(i,j)=s(xp(i,j))- yp1, yp2, yp3
vectors (or matrices) of same size than
xp, elementwise evaluation of the successive derivatives ofsonxp
Description
Given three vectors (x,y,d) defining a spline or
sub-spline function (see splin) with
yi=s(xi), di = s'(xi) this function evaluates
s (and s', s'', s''' if needed) at
xp(i) :

The out_mode parameter set the evaluation rule
for extrapolation, i.e. for xp(i) not in [x1,xn]
:
- "by_zero"
an extrapolation by zero is done
- "by_nan"
extrapolation by Nan
- "C0"
the extrapolation is defined as follows :
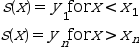
- "natural"
the extrapolation is defined as follows (p_i being the polynomial defining
son [x_i,x_{i+1}]) :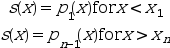
- "linear"
the extrapolation is defined as follows :
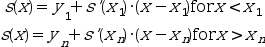
- "periodic"
sis extended by periodicity.
Examples
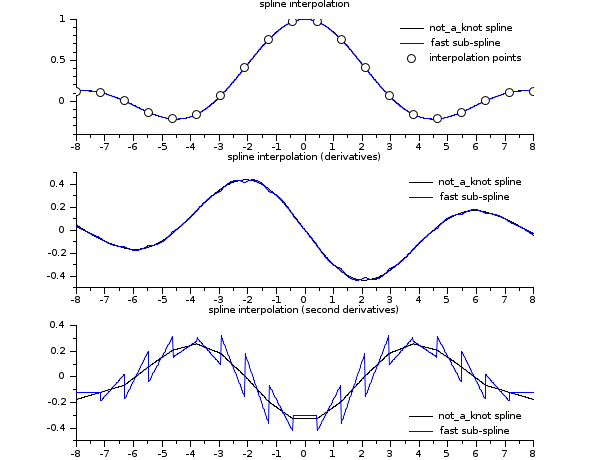
// see the examples of splin and lsq_splin // an example showing C2 and C1 continuity of spline and subspline a = -8; b = 8; x = linspace(a,b,20)'; y = sinc(x); dk = splin(x,y); // not_a_knot df = splin(x,y, "fast"); xx = linspace(a,b,800)'; [yyk, yy1k, yy2k] = interp(xx, x, y, dk); [yyf, yy1f, yy2f] = interp(xx, x, y, df); clf() subplot(3,1,1) plot2d(xx, [yyk yyf]) plot2d(x, y, style=-9) legends(["not_a_knot spline","fast sub-spline","interpolation points"],... [1 2 -9], "ur",%f) xtitle("spline interpolation") subplot(3,1,2) plot2d(xx, [yy1k yy1f]) legends(["not_a_knot spline","fast sub-spline"], [1 2], "ur",%f) xtitle("spline interpolation (derivatives)") subplot(3,1,3) plot2d(xx, [yy2k yy2f]) legends(["not_a_knot spline","fast sub-spline"], [1 2], "lr",%f) xtitle("spline interpolation (second derivatives)")
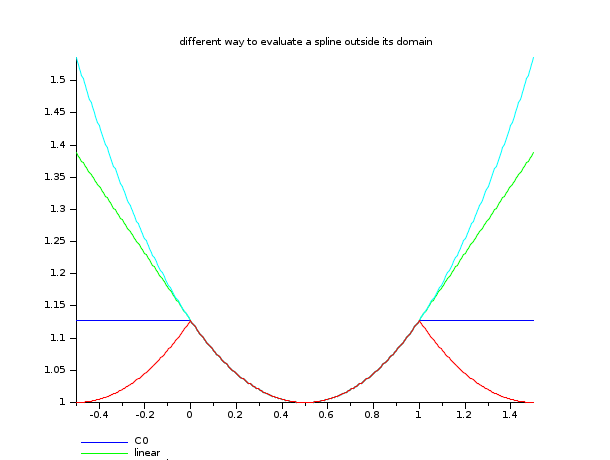
// here is an example showing the different extrapolation possibilities x = linspace(0,1,11)'; y = cosh(x-0.5); d = splin(x,y); xx = linspace(-0.5,1.5,401)'; yy0 = interp(xx,x,y,d,"C0"); yy1 = interp(xx,x,y,d,"linear"); yy2 = interp(xx,x,y,d,"natural"); yy3 = interp(xx,x,y,d,"periodic"); clf() plot2d(xx,[yy0 yy1 yy2 yy3],style=2:5,frameflag=2,leg="C0@linear@natural@periodic") xtitle(" different way to evaluate a spline outside its domain")
History
| Version | Description |
| 5.4.0 | previously, imaginary part of input arguments were implicitly ignored. |
| Report an issue | ||
| << eval_cshep2d | Interpolation | interp1 >> |