Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
However, this page did not exist in the previous stable version.
oldbesseli
第1種の修正ベッセル関数 (I_alpha).
oldbesselj
第1種のベッセル関数 (J_alpha).
oldbesselk
第2種の修正ベッセル関数 (K_alpha).
oldbessely
第2種のベッセル関数 (Y_alpha).
呼び出し手順
y = oldbesseli(alpha,x) y = oldbesseli(alpha,x,ice) y = oldbesselj(alpha,x) y = oldbesselk(alpha,x) y = oldbesselk(alpha,x,ice) y = oldbessely(alpha,x)
パラメータ
- x
real vector with non negative entries
- alpha
real vector with non negative entries regularly spaced with increment equal to one
alpha=alpha0+(n1:n2)- ice
integer flag, with default value 1
説明
これらの関数は古い関数であり, besseli, besselj, besselk, bessely を代わりに使用してください. しかし,これらの2組の関数の構文は異なっていることに注意してください.
oldbesseli(alpha,x) computes modified Bessel
functions of the first kind (I sub alpha), for real, non-negative order
alpha and real non negative argument
x. besseli(alpha,x,2) computes
besseli(alpha,x).*exp(-x).
oldbesselj(alpha,x) computes Bessel functions of
the first kind (J sub alpha), for real, non-negative order
alpha and real non negative argument
x.
oldbesselk(alpha,x) computes modified Bessel
functions of the second kind (K sub alpha), for real, non-negative order
alpha and real non negative argument
x. besselk(alpha,x,2) computes
besselk(alpha,x).*exp(x).
oldbessely(alpha,x) computes Bessel functions of
the second kind (Y sub alpha), for real, non-negative order
alpha and real non negative argument
x.
alpha and x may be vectors.
The output is m-by-n with m
= size(x,'*'), n = size(alpha,'*') whose
(i,j) entry is
oldbessel?(alpha(j),x(i)).
Remarks
Y_alpha and J_alpha Bessel functions are 2 independant solutions of the Bessel 's differential equation :
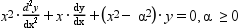
K_alpha and I_alpha modified Bessel functions are 2 independant solutions of the modified Bessel 's differential equation :
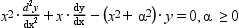
Examples
// example #1: display some I Bessel functions x = linspace(0.01,10,5000)'; y = oldbesseli(0:4,x); ys = oldbesseli(0:4,x,2); clf() subplot(2,1,1) plot2d(x,y, style=2:6, leg="I0@I1@I2@I3@I4", rect=[0,0,6,10]) xtitle("Some modified Bessel functions of the first kind") subplot(2,1,2) plot2d(x,ys, style=2:6, leg="I0s@I1s@I2s@I3s@I4s", rect=[0,0,6,1]) xtitle("Some modified scaled Bessel functions of the first kind") // example #2 : display some J Bessel functions x = linspace(0,40,5000)'; y = besselj(0:4,x); clf() plot2d(x,y, style=2:6, leg="J0@J1@J2@J3@J4") xtitle("Some Bessel functions of the first kind") // example #3 : use the fact that J_(1/2)(x) = sqrt(2/(x pi)) sin(x) // to compare the algorithm of besselj(0.5,x) with // a more direct formula x = linspace(0.1,40,5000)'; y1 = besselj(0.5, x); y2 = sqrt(2 ./(%pi*x)).*sin(x); er = abs((y1-y2)./y2); ind = find(er > 0 & y2 ~= 0); clf() subplot(2,1,1) plot2d(x,y1,style=2) xtitle("besselj(0.5,x)") subplot(2,1,2) plot2d(x(ind), er(ind), style=2, logflag="nl") xtitle("relative error between 2 formulae for besselj(0.5,x)") // example #4: display some K Bessel functions x = linspace(0.01,10,5000)'; y = besselk(0:4,x); ys = besselk(0:4,x,1); clf() subplot(2,1,1) plot2d(x,y, style=0:4, leg="K0@K1@K2@K3@K4", rect=[0,0,6,10]) xtitle("Some modified Bessel functions of the second kind") subplot(2,1,2) plot2d(x,ys, style=0:4, leg="K0s@K1s@K2s@K3s@K4s", rect=[0,0,6,10]) xtitle("Some modified scaled Bessel functions of the second kind") // example #5: plot severals Y Bessel functions x = linspace(0.1,40,5000)'; // Y Bessel functions are unbounded for x -> 0+ y = bessely(0:4,x); clf() plot2d(x,y, style=0:4, leg="Y0@Y1@Y2@Y3@Y4", rect=[0,-1.5,40,0.6]) xtitle("Some Bessel functions of the second kind")
Authors
W. J. Cody, L. Stoltz (code from Netlib (specfun))
| << legendre | Special Functions | Randlib >> |