Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
bsplin3val
3d spline arbitrary derivative evaluation function
Calling Sequence
[dfp]=bsplin3val(xp,yp,zp,tl,der)
Arguments
- xp, yp, zp
real vectors or matrices of same size
- tl
tlist of type "splin3d", defining a 3d tensor spline (called
sin the following)- der
vector with 3 components
[ox,oy,oz]defining which derivative ofsto compute.- dfp
vector or matrix of same format than
xp,ypandzp, elementwise evaluation of the specified derivative ofson these points.
Description
While the function interp3d may
compute only the spline s and its first derivatives,
bsplin3val may compute any derivative of
s. The derivative to compute is specified by the
argument der=[ox,oy,oz] :
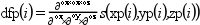
So der=[0 0 0] corresponds to
s, der=[1 0 0] to
ds/dx, der=[0 1 0] to
ds/dy, der=[1 1 0] to
d2s/dxdy, etc...
For a point with coordinates (xp(i),yp(i),zp(i)) outside the grid, the function returns 0.
Examples
deff("v=f(x,y,z)","v=cos(x).*sin(y).*cos(z)"); deff("v=fx(x,y,z)","v=-sin(x).*sin(y).*cos(z)"); deff("v=fxy(x,y,z)","v=-sin(x).*cos(y).*cos(z)"); deff("v=fxyz(x,y,z)","v=sin(x).*cos(y).*sin(z)"); deff("v=fxxyz(x,y,z)","v=cos(x).*cos(y).*sin(z)"); n = 20; // n x n x n interpolation points x = linspace(0,2*%pi,n); y=x; z=x; // interpolation grid [X,Y,Z] = ndgrid(x,y,z); V = f(X,Y,Z); tl = splin3d(x,y,z,V,[5 5 5]); // compute f and some derivates on a point // and compare with the spline interpolant xp = grand(1,1,"unf",0,2*%pi); yp = grand(1,1,"unf",0,2*%pi); zp = grand(1,1,"unf",0,2*%pi); f_e = f(xp,yp,zp) f_i = bsplin3val(xp,yp,zp,tl,[0 0 0]) fx_e = fx(xp,yp,zp) fx_i = bsplin3val(xp,yp,zp,tl,[1 0 0]) fxy_e = fxy(xp,yp,zp) fxy_i = bsplin3val(xp,yp,zp,tl,[1 1 0]) fxyz_e = fxyz(xp,yp,zp) fxyz_i = bsplin3val(xp,yp,zp,tl,[1 1 1]) fxxyz_e = fxxyz(xp,yp,zp) fxxyz_i = bsplin3val(xp,yp,zp,tl,[2 1 1])
Authors
- R.F. Boisvert, C. De Boor (code from the CMLIB fortran lib)
- B. Pincon (scilab interface)
| << Interpolation | Interpolation | cshep2d >> |