Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
interp2d
bicubic spline (2d) evaluation function
Calling Sequence
[zp[,dzpdx,dzpdy[,d2zpdxx,d2zpdxy,d2zpdyy]]]=interp2d(xp,yp,x,y,C [,out_mode])
Arguments
- xp, yp
real vectors or matrices of same size
- x,y,C
real vectors defining a bicubic spline or sub-spline function (called
sin the following)- out_mode
(optional) string defining the evaluation of
soutside [x(1),x(nx)]x[y(1),y(ny)]- zp
vector or matrix of same format than
xpandyp, elementwise evaluation ofson these points.- dzpdx, dzpdy
vectors (or matrices) of same format than
xpandyp, elementwise evaluation of the first derivatives ofson these points.- d2zpdxx, d2zpdxy, d2zpdyy
vectors (or matrices) of same format than
xpandyp, elementwise evaluation of the second derivatives ofson these points.
Description
Given three vectors (x,y,C) defining a bicubic
spline or sub-spline function (see splin2d)
this function evaluates s (and ds/dx,
ds/dy, d2s/dxx, d2s/dxy, d2s/dyy if needed) at
(xp(i),yp(i)) :
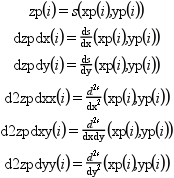
The out_mode parameter defines the evaluation
rule for extrapolation, i.e. for (xp(i),yp(i)) not in
[x(1),x(nx)]x[y(1),y(ny)]:
- "by_zero"
an extrapolation by zero is done
- "by_nan"
extrapolation by Nan
- "C0"
the extrapolation is defined as follows :
- "natural"
the extrapolation is done by using the nearest bicubic-patch from (x,y).
- "periodic"
sis extended by periodicity.
Examples
// see the examples of splin2d // this example shows some different extrapolation features // interpolation of cos(x)cos(y) n = 7; // a n x n interpolation grid x = linspace(0,2*%pi,n); y = x; z = cos(x')*cos(y); C = splin2d(x, y, z, "periodic"); // now evaluate on a bigger domain than [0,2pi]x [0,2pi] m = 80; // discretisation parameter of the evaluation grid xx = linspace(-0.5*%pi,2.5*%pi,m); yy = xx; [XX,YY] = ndgrid(xx,yy); zz1 = interp2d(XX,YY, x, y, C, "C0"); zz2 = interp2d(XX,YY, x, y, C, "by_zero"); zz3 = interp2d(XX,YY, x, y, C, "periodic"); zz4 = interp2d(XX,YY, x, y, C, "natural"); clf() subplot(2,2,1) plot3d(xx, yy, zz1, flag=[2 6 4]) xtitle("extrapolation with the C0 outmode") subplot(2,2,2) plot3d(xx, yy, zz2, flag=[2 6 4]) xtitle("extrapolation with the by_zero outmode") subplot(2,2,3) plot3d(xx, yy, zz3, flag=[2 6 4]) xtitle("extrapolation with the periodic outmode") subplot(2,2,4) plot3d(xx, yy, zz4, flag=[2 6 4]) xtitle("extrapolation with the natural outmode") show_window()
See Also
Authors
B. Pincon
| << interp1 | Interpolation | interp3d >> |