Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
DLR
Discrete transfer function
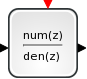
Block Screenshot
Contents
Palette
Description
This block realizes a SISO linear system represented by its rational transfer function (in the symbolic variable z). The rational function must be proper.
Dialog box
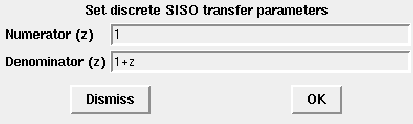
Numerator (z)
This parameter sets the numerator of the transfer function.
This must be a polynomial inz .
Properties : Type 'pol' of size 1.
Denominator (z)
This parameter sets the denominator of the transfer function.
This must be a polynomial inz .
Properties : Type 'pol' of size 1.
Default properties
always active: no
direct-feedthrough: no
zero-crossing: no
mode: no
regular inputs:
- port 1 : size [1,1] / type 1
regular outputs:
- port 1 : size [1,1] / type 1
number/sizes of activation inputs: 1
number/sizes of activation outputs: 0
continuous-time state: no
discrete-time state: yes
object discrete-time state: no
name of computational function: dsslti4
Interfacing function
SCI/modules/scicos_blocks/macros/Linear/DLR.sci
Computational function
SCI/modules/scicos_blocks/src/c/dsslti4.c (Type 4)
| << DELAY_f | Discrete time systems palette | DLRADAPT_f >> |