gallery

Arguments

name

matrix name available in the following list: "cauchy", "circul" and "ris

n1, ..., nn

double, scalars or vectors depend on the name of matrix

g

generated matrix

Description

g = gallery(name, n1, ..., nn) generates a name matrix. n1, ..., nn arguments depend on the generated matrix (see *name* matrix sections below for more details).

g = gallery(3) is a badly conditioned 3-by-3 matrix.

g = gallery(5) creates a 5-by-5 matrix with an interesting eigenvalue problem.

Cauchy matrix

g = gallery("cauchy", x [, y]) creates a n-by-n Cauchy matrix. x and y are vectors of length n. If x is scalar, then it will be interpreted as 1:x (same behavior for y).

The Cauchy matrix is defined by g(i,j) = 1/(x(i) + y(j)).

g = gallery("cauchy", x) computes g(i,j) = 1/(x(i) + x(j)).

Circulant matrix

g = gallery("circul", x) creates a n-by-n Circulant matrix whose first row is given by x. x is vector of length n. If x is scalar, then it will be interpreted as 1:x.

A circulant matrix is a square matrix whose each row is obtained from the previous one by circular permutation (right shift):

.

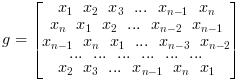Ris matrix

g = gallery("ris", n) creates a n-by-n Ris matrix. This matrix is symectric n-by-n Hankel matrix with g(i,j) = 0.5/(n - i - j + 1.5). Its eigenvalues have the property of clustering near +/- pi/2.

Examples

Cauchy matrix

g = gallery("cauchy", 3)
g = gallery("cauchy", 1:3, 2:4)

Circulant matrix

g = gallery("circul", 5)
g = gallery("circul", [4 8 -1])

Ris matrix

g = gallery("ris", 3)

See also

• toeplitz — Toeplitz matrix (chosen constant diagonal bands)
• hilbm — Hilbert matrix
• invhilb — Inverse of the Hilbert matrix
• magic — Magic square
• vander — Vandermonde matrix
• frank — Frank matrix
• pascal — Pascal matrix
• hankel — Hankel matrix

History