polyfit
Polynomial curve fitting
Syntax
p = polyfit(x, y, n [,w]) [p, S] = polyfit(x, y, n [,w]) [p, S, mu] = polyfit(x, y, n [,w])
Arguments
- x
real or complex vector/matrix
- y
real or complex vector/matrix.
ymust have the same size asx- n
an integer, n>=0. It is a degree of the fitting polynomial. Or a polynom. In the case,
polyfitextracts the degree of polynom and returns a polynom containing the coefficients.- w
real vector/matrix, the weights to apply to each
yvalue. Default value: ones(x).- p
a
1xn+1real or complex vector or polynom, the polynomial coefficients- S
a structure containing the following fields:
- R
a matrix of doubles, the triangular factor R form the qr decomposition
- df
a real, the degrees of freedom
- normr
a real, the norm of the residuals
- mu
a
1x2vector.mu(1)ismean(x)andmu(2)isstdev(x)
Description
p = polyfit(x, y, n) returns a vector of coefficients of a polynomial p(x)
of degree n:
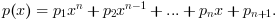
Depending on the type of n, p will be a real or complex vector or a polynom.
p can be used with polyval function to evaluate the polynomial at the data points.
[p, S] = polyfit(x, y, n) returns a vector of coefficients of a polynomial and a structure
S that can be used with polyval to compute the estimated error of the predicted values.
[p, S, mu] = polyfit(x, y, n) returns a third output argument mu
containing [mean(x), stdev(x)]. x is centered at zero and scaled to have unit standard deviation.
p = polyfit(x, y, n, w) specifies weights to apply to each y value.
Examples
Some examples use lambda functions.
example 1 - p = polyfit(x, y, n)
x = 1:5; // Use lambda function y = #(x) -> (-2*x.^4 + x.^3 - 5 * x.^2 + 6 *x -2); p = polyfit(x, y(x), 3) xx = linspace(1, 5, 100); yy = polyval(p, xx); plot(x, y(x), "b.", "thickness", 2); plot(xx, yy, "r");
example 2 - p = polyfit(x, y, n) with n a polynom
function r=y(x) r = -2*x.^4 + x.^3 - 5 * x.^2 + 6 *x -2; endfunction x = 1:5; p = polyfit(x, y(x), %s^3) xx = linspace(1, 5, 100); yy = polyval(p, xx); plot(x, y(x), "b.", "thickness", 2); plot(xx, yy, "r");
example 3 - [p, S, mu] = polyfit(x, y, n)
x = 0:10; // Use lambda function y = #(x) -> (x.^3 - 3*x + 2); [p, S, mu] = polyfit(x, y(x), 2) xx = linspace(0, 10, 100); yy = polyval(p, xx, S, mu); plot(x, y(x), "b.", "thickness", 2); plot(xx, y(xx), "g"); plot(xx, yy, "r");
example 4 - p = polyfit(x, y, n, w)
x = [1 1.5 2.1 3.3 4 6]; y = 39 *x - [22 28 12 20 -2 22]; w = [1 0.25 0.11 0.8 0.2 1] p = polyfit(x,y,1) pw = polyfit(x,y,1,w) xx = 1:6; yy = polyval(p, xx); // unweighted yyw = polyval(pw, xx); // weighted plot(x, y, ".") plot(xx, yy, "k") plot(xx, yyw, "r") legend(["data"; "unweighted"; "weight"], "in_upper_left")
History
| Версия | Описание |
| 2025.0.0 | Introduction in Scilab. |
| 2025.1.0 | Weights (w) for y values are now managed. |
| Report an issue | ||
| << kmeans | Statistics | polyval >> |