black
Black-Nichols diagram of a linear dynamical system
Syntax
black(sl) black(sl, fmin, fmax) black(sl, fmin, fmax, step) black(sl, frq) black(frq, db, phi) black(frq, repf) black(.., comments)
Arguments
- sl
A siso or simo linear dynamical system, in state space, transfer function or zpk representations, in continuous or discrete time.
- fmin,fmax
real scalars (frequency bounds)
- frq
row vector or matrix (frequencies)
- db, phi
row vectors or matrices of modulus (in dB) and phases (in degrees). One row for each response.
- repf
row or matrix of complex frequency response(s). One row for each response.
- step
real: (logarithmic) discretization step. See calfrq for the choice of default value.
- comments
vector of character strings: captions.
Description
Black's diagram (Nichols'chart) for a linear dynamical system .
sl can be a continuous-time or
discrete-time SIMO system given by its state space,
rational transfer function (see syslin) or zpk representation. In case of
multi-output the outputs are plotted with different
colors.
The frequencies are given by the bounds
fmin,fmax (in Hz) or
by a row-vector (or a matrix for multi-output)
frq.
To plot the grid of iso-gain and iso-phase of
y/(1+y) use nicolschart().
Default values for fmin and
fmax are 1.d-3,
1.d+3 if sl is continuous-time or
1.d-3, 0.5/sl.dt (nyquist frequency)
if sl is discrete-time.
Examples
//Black diagram s=poly(0,'s'); sl=syslin('c',5*(1+s)/(.1*s.^4+s.^3+15*s.^2+3*s+1)) clf();black(sl,0.01,10);
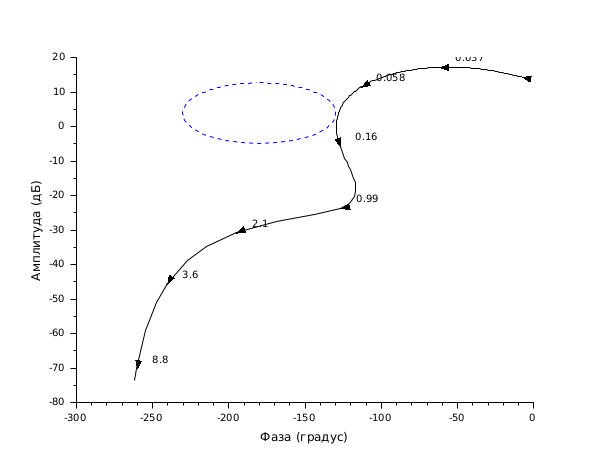
//Black diagram with Nichols chart as a grid s=poly(0,'s'); Plant=syslin('c',16000/((s+1)*(s+10)*(s+100))); //two degree of freedom PID tau=0.2;xsi=1.2; PID=syslin('c',(1/(2*xsi*tau*s))*(1+2*xsi*tau*s+tau.^2*s.^2)); clf(); black([Plant;Plant*PID ],0.01,100,["Plant";"Plant and PID corrector"]); //move the caption in the lower right corner ax=gca();Leg=ax.children(1); Leg.legend_location="in_lower_right"; nicholschart(colors=color('light gray')*[1 1])
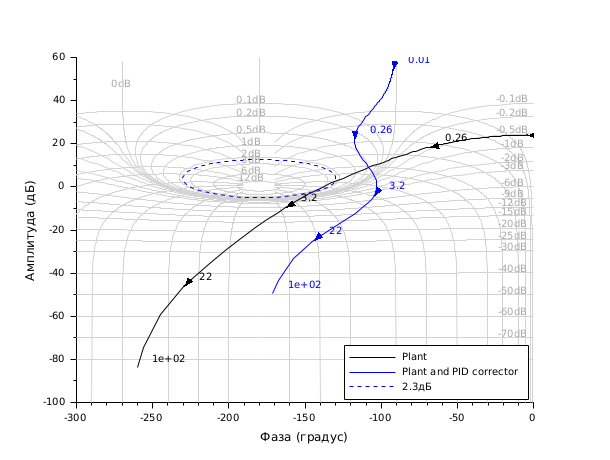
See also
History
| Версия | Описание |
| 6.0 | handling zpk representation |
| Report an issue | ||
| << Frequency Domain | Frequency Domain | bode >> |