DELAYV_f
Variable delay
Block Screenshot

Contents
Description
The Variable Delay block can be used to simulate a variable time delay between an action and its effect. The block might be used, for example, to model a system with a pipe where the speed of a motor pumping fluid in the pipe is variable.
The block accepts two inputs and one output: the first input is the signal u(t) that passes through the block (data input); the second input is the variable time delay τ(t).
The output activation ports trigger every
"Max delay"/length("Register initial condition").
The input activation port and the first output activation port are meant to be linked, to get the variations of the input.
The final delay is: τ(t) + "Max delay"/length("Register initial condition").
Parameters
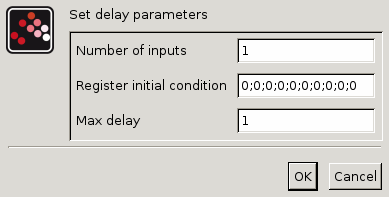
Number of inputs
Set the vector size of the first regular input and the vector size of the regular output port.
Properties : Type 'vec' of size 1.
Register initial condition
Set the length and the initial conditions of the register.
Properties : Type 'vec' of size -1.
Max delay
It defines the largest value the time delay input can have.The value cannot be negative.
Properties : Type 'vec' of size 1.
Default properties
always active: no
direct-feedthrough: yes
zero-crossing: no
mode: no
regular inputs:
- port 1 : size [1,1] / type 1
- port 2 : size [1,1] / type 1
regular outputs:
- port 1 : size [1,1] / type 1
number/sizes of activation inputs: 1
number/sizes of activation outputs 2
continuous-time state: no
discrete-time state: yes
object discrete-time state: no
name of computational function: delayv
Interfacing function
SCI/modules/scicos_blocks/macros/Linear/DELAYV_f.sci
Computational function
SCI/modules/scicos_blocks/src/fortran/delayv.f (Type 1)
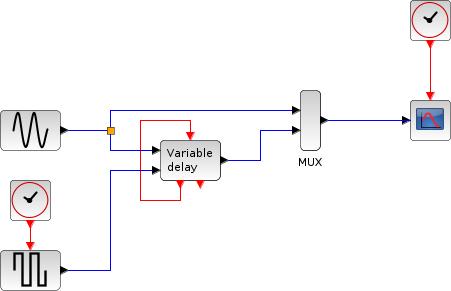
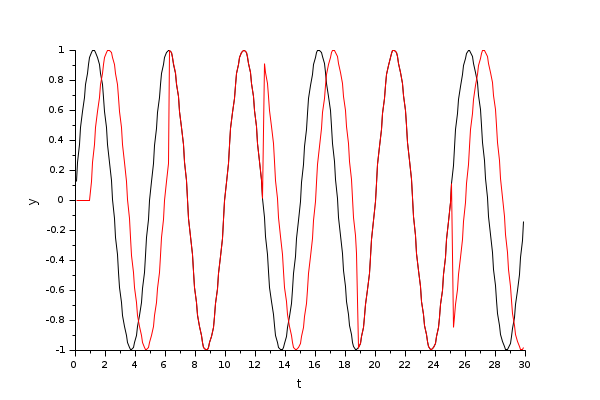
Variable delay example
In this example, the sine function (in black) est delayed alternatively by 0 and 1 second. The amplitude of the GENSQR_f block is fixed at 2, but the "Max delay" parameter of the DELAVV_f block restrains that value to 1. We see that with every time GENSQR_f is activated (every 2*π seconds), the delay changes: the curves overlap (delay=0) and are shifted (delay=1) in turn.
| Report an issue | ||
| << Discrete_pal | Discrete time systems palette | DELAY_f >> |