Events
Specifying a user events function
Syntax
... = solver( ... , events = evFn) ... = solver( ... , events = evFn, nbEvents = nb) ... = solver( ... , events = evFn, nbEvents = nb, evDir = dir) ... = solver( ... , events = evFn, nbEvents = nb, evDir = dir, evTerm = term)
Arguments
| evFn | A Scilab function, a list, a string. |
| nb | The size of the vector yielded by the DLL entrypoint when evFn is a string. |
| dir,term | Two vectors of length nb, when evFn is a string |
Description
While integrating an ODE or a DAE, the solver can also find the roots of a set of nb user-defined functions that depend both on t and on the solution vector y (and also y' for a DAE). The number of these roots or event functions is arbitrary, and if more than one function is found to have a root in any given interval, the various root locations are found and reported in the order that they occur on the t axis, in the direction of integration. The syntax
[t,y,info] = solver(..., events = evFn) sol = solver(..., events = evFn)
for an ODE or a DAE, allows to recover the event locations
and the vanishing function(s) in the respective fields te,ye,ype,ie of the output
arguments info or sol. Field te is a vector giving the time of
events, ye an array with solution at each event time
(ype gives the derivative of the solution in the case of a DAE)
and ie is a matrix with as many lines as the number of event functions and as many columns
of events having occurred. Typically info.ie(i,j) will be 1 or -1 when event function i
vanishes at time info.te(j) with corresponding sign of its derivative (two event functions can vanish
at the same time).
General information about the different ways of providing a user function (and
eventual user parameters) is given in the User Functions help page.
Event function given as a Scilab function
In that case evFn is a Scilab function with prototype
for an ODE or a DAE, respectively, where eq(i) = 0 when event i
occurs. The two other optional outputs term,dir, if present, will be used only at solver initialization. The vector term is a boolean
vector, with term(i) = 1 if integration has to be stopped when event i occurs. Vector dir allows to
select event direction, where term(i) can take the values -1,1 if solution has to be decreasing or increasing or 0
if direction does not matter. If the corresponding behavior does not matter, dir or both term,dir outputs can be omitted in the function
prototype.
For example, in order to find all points in [0,10] where the solution of Van Der Pol equation veryfies y(t)=1, we use the following code:
function eq=g1(t, v) eq = v(1)-1; end function [eq, term, dir]=g2(t, v) dir = -1; term = 1; eq = v(1)-1; end [t, v, info] = cvode(%SUN_vdp1, [0 10], [0; 2], events = g1); plot(info.te, info.ye(1,:),"or",t,v) [t, v, info] = cvode(%SUN_vdp1, [0 10], [0; 2], events = g2); plot(info.te, info.ye(1,:),"xr","marksize",10)
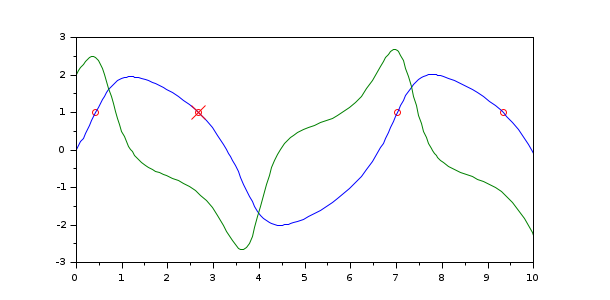
In this other example, we find the time and value of the maximum of 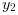 in SIR model by finding the
time when
in SIR model by finding the
time when 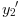 vanishes:
vanishes:
function eq=g(t, y, yp) eq = yp(2) end y0 = [1-1e-6;1e-6;0]; yp0 = [-2e-7;1.5e-7;5e-8]; [t, y, info] = ida(%SUN_sir, [0,200], y0, yp0, events=g); clf plot(t, y, info.te, info.ye(2),'or') xstring(info.te, info.ye(2), msprintf("t=%g, y=%g", info.te, info.ye(2)))
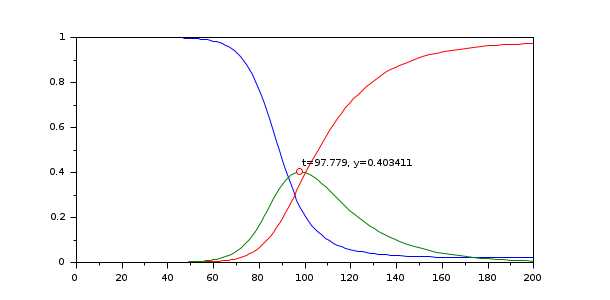
Event function given as a SUNDIALS DLL entrypoint
In that case evFn must have the C prototype
int sunEvent(realtype t, N_Vector Y, realtype *gout, void *user_data) int sunEvent(realtype t, N_Vector Y, N_Vector Yp, realtype *gout, void *user_data)
for an ODE or a DAE, respectively. When calling the solver the option nEvents
must be set in order to define the number of events. If
the direction of the events have to be set or if some events should
terminate the solver iterations, the evDir and evTerm can be used
and the values of dir and term follow the same convention as when evFn is
a Scilab function. See the examples below (Van Der Pol ODE and SIR model DAE):
code=[ "#include <nvector/nvector_serial.h>" "int sunEvent(realtype t, N_Vector Y, realtype* gout, void* user_data)" "{ " "double *y = NV_DATA_S(Y);" "gout[0] = y[0]-1.7;" "return 0;" "}"]; mputl(code,"code.c"); //create the C file SUN_Clink("sunEvent","code.c",load=%t); // compile and link [t, y, info1] = cvode(%SUN_vdp1,[0 10],[2;1], nbEvents=1, events="sunEvent"); [t, y, info2] = cvode(%SUN_vdp1,[0 10],[2;1], nbEvents=1, events="sunEvent", evDir=-1); [t, y, info3] = cvode(%SUN_vdp1,[0 10],[2;1], nbEvents=1, events="sunEvent", evDir=-1, evTerm=1); disp(info1.ye, info2.ye, info3.ye)
code=[ "#include <nvector/nvector_serial.h>" "int sunEvent(realtype t, N_Vector Y, N_Vector Yd, realtype* gout, void* user_data)" "{ " "double *yd = NV_DATA_S(Yd);" "gout[0] = yd[1];" "return 0;" "}"]; mputl(code,"code.c"); //create the C file SUN_Clink("sunEvent","code.c",load=%t); // compile and link y0 = [1-1e-6;1e-6;0]; yp0 = [-2e-7;1.5e-7;5e-8]; [t, y, info] = ida(%SUN_sir, [0,200], y0, yp0, events="sunEvent", nbEvents=1); disp(info.te, info.ype)
See also
- arkode — SUNDIALS ordinary differential equation additive Runge-Kutta solver
- cvode — SUNDIALS ordinary differential equation solver
- ida — SUNDIALS differential-algebraic equation solver
- User functions — Coding user functions used by SUNDIALS solvers
- Options (ODE and DAE solvers) — Changing the default behavior of solver
- SUN_Clink — Compiling and linking a C user function
| Report an issue | ||
| << Complex solutions | Options, features and user functions | Jacobian >> |