lattp
Identification of MA part of a vector ARMA process
Syntax
[la,lb]=lattp(n,p,cov)
Arguments
- n
maximum order of the filter
- p
fixed dimension of the MA part. If
p= -1, the algorithm reduces to the classical Levinson recursions.- cov
matrix containing the
Rk's (d*dmatrices for a d-dimensional process).It must be given the following way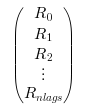
- la
list-type variable, giving the successively calculated polynomials (degree 1 to degree p),with coefficients Ak
Description
This function identifies the MA part of a vector ARMA(n,p) process.
Example
See also
| Report an issue | ||
| << lattn | Identification | mrfit >> |