fchamp
2次元1階常微分方程式(ODE)のフィールド方向
呼び出し手順
fchamp(f, t, xr, yr, [arfact, rect, strf]) fchamp(f, t, xr, yr, <opt_args>)
引数
- f
外部ルーチン (関数または文字列) または ODE を記述するリスト.
- -
関数名
fとすることができ, この際,fはy=f(t,xy [p1,..pn])という型の関数と仮定されます.fは大きさ 2 の列ベクトルを返し, そのベクトルは点xy=[x,y]の時刻tにおける方向フィールドfの値を指定します.- -
リスト型のオブジェクト
list(f,P1,..Pn)とすることも可能で, この場合,fはy=f(t,xy,p1,..pn)という型の関数,Piはパラメータpiの値を指定します.
- t
選択された時間.
- xr,yr
大きさ
n1およびn2の行ベクトルで, 方向フィールドが計算されるグリッドを定義します.- <opt_args>
一連の命令
key1=value1,key2=value2... を表します. ただし,key1,key2,...は以下のどれかとします:arfact,rect,strf(以下参照).- arfact,rect,strf
オプションの引数,
champ参照.
説明
fchamp は,外部関数fで定義された
2次元1階常微分方程式(ODE)のフィールド方向を描画する際に使用されます.
 | ODEが自律的な場合, 引数 fは不要ですが,
指定する必要があることに注意してください. |
コマンド fchamp() を入力するとデモを参照できます.
例
deff("[xdot] = derpol(t,x)",.. ["xd1 = x(2)";.. "xd2 = -x(1) + (1 - x(1)**2)*x(2)";.. "xdot = [ xd1 ; xd2 ]"]) xf= -1:0.1:1; yf= -1:0.1:1; fchamp(derpol,0,xf,yf)
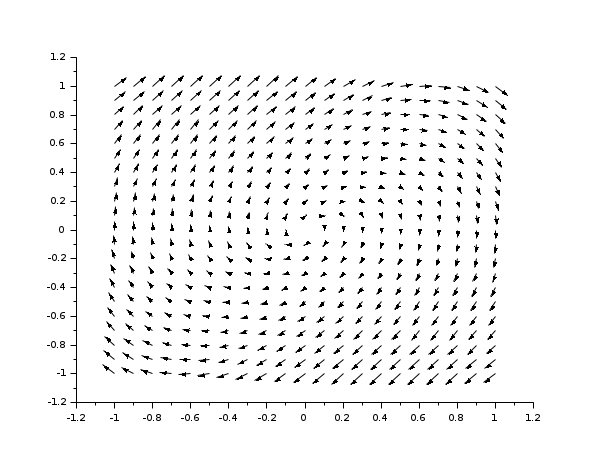
deff("[xdot] = derpol(t,x)",.. ["xd1 = x(2)";.. "xd2 = -x(1) + (1 - x(1)**2)*x(2)";.. "xdot = [ xd1 ; xd2 ]"]) xf= -1:0.1:1; yf= -1:0.1:1; clf() fchamp(derpol,0,xf,yf,1,[-2,-2,2,2],"011")
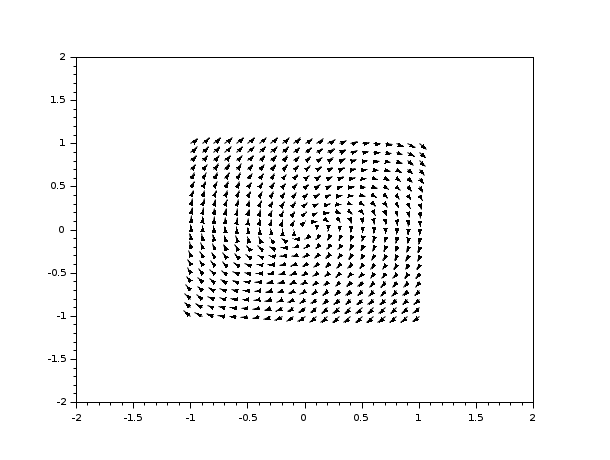
参照
- champ — 2次元ベクトルフィールドのプロット
- champ_properties — 2次元ベクトルフィールドエンティティプロパティの説明
- xarrows — 2Dまたは3Dで矢印を描画
- Arrowed polyline — Polylineエンティティプロパティの説明
| Report an issue | ||
| << errbar | 2d_plot | fec >> |