Sensitivity (DAE)
Forward Sensitivity computation with ida
Syntax
[t,y,info] = ida(res, tspan, y0, yp0, sensPar = pvalue, options) sol = ida( ... , sensPar = pvalue, options)
Arguments
| pvalue | a real double array: the value of parameters with respect to which sensitivity is computed |
| options | a sequence of optional named arguments (see the solvers options) and below for sensitivity specific options. |
| t | vector of time points used by the solver. |
| y | array of solution at time values in t |
| info | MList of |
| sol | MList of |
Description
While integrating a DAE where residual F(t,y,y',p) depends on a vector p of parameters, ida can compute simultaneously the
solution vectors y, y' at given time points and also 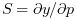 ,
, 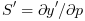 the derivatives of y and y' with
respect to p, i.e. the sensitivity matrix and its time derivative.
This amounts to augment the original DAE with the sensitivity residual, which is obtained by formal derivation of the original DAE residual
with respect to p:
the derivatives of y and y' with
respect to p, i.e. the sensitivity matrix and its time derivative.
This amounts to augment the original DAE with the sensitivity residual, which is obtained by formal derivation of the original DAE residual
with respect to p:
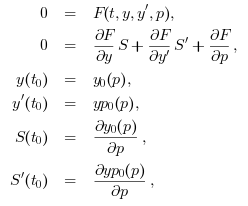
The sensitivity matrix is typically used when solving identification parameter problems, for example nonlinear regression, and it can serve both aspects of the problem solution, i.e. qualitative and quantitative: studying the sensitivity on the time span can help to state identifiability of the parameters whereas computing the sensitivity at precise time points of measurements allows to compute the gradient of the squared norm of the observation residual.
When the residual of the DAE is
explicitely known then the exact sensitivity equation residual can be provided (see the sensRes below), but ida can also
approximate it by approximating directional derivatives by finite difference quotients. However, better precision is always obtained with
exact derivatives. In the example below we compute the sensitivity equation residual by the complex step method, which is exact up to
machine precision.
The sensitivity computation is triggered by using the sensPar option:
[t,y,info] = ida(res, tspan, y0, yp0, sensPar = pvalue) sol = ida(res, tspan, y0, yp0, sensPar = pvalue
where the sensitivity of the solution and its derivative are retrieved in the "s" and "sp" fields of either the info or sol output argument.
When the residual of the DAE is yielded by a Scilab function, the prototype of res must include a formal
input argument after the usual (t,y,yp) triplet (denoted p below), which will contain the parameter values. Additionnal user parameters
must be given as explained in the User functions help page :
dydt = res(t, y, yp, p, ...)
When the residual of the DAE is yielded by a DLL entry point, as only one array of double values can be passed,
complimentary user parameters must be passed together with sensitivity parameters in the same vector. The actual sensitivity
parameters can be precised by using the sensParIndex (see below).
The sensitivity related output arguments s,sp and se (when events occur) can be recovered in the solution output as complimentary fields. Note that the yielded info.s,info.sp arrays have dimensions (length(y0), length(p), length(t)) but singleton dimension is squeezed when p is a scalar.
Example
Here we compute the sensitivity of the solution of the SIR epidemiologic system (written as a DAE) with respect to parameter β and γ. Option yS0 and ypS0 allow to give
the initial values of the sensitivity and of its derivative. When y0 does not depend on the parameters then yS0 is the null matrix and does not need to be given,
but ypS0 has always to be given. In the code below this value is computed together with yp0 thanks to the calcIC option, once the algebraic state y_3 has been
indicated by using the yIsAlgebric option.
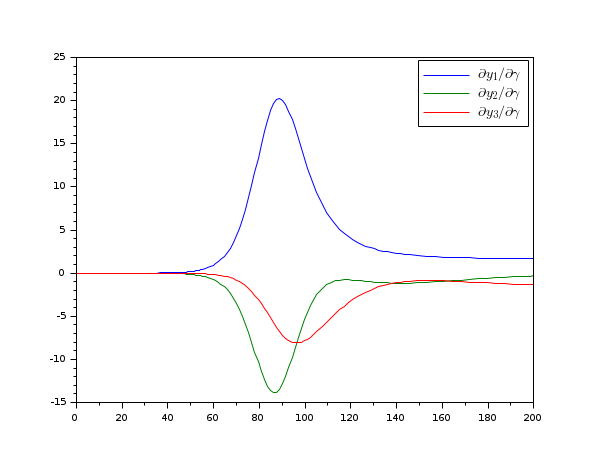
function dydt=rsir(t, y, yp, p) β = p(1); γ = p(2); dydt = [-β*y(1)*y(2)-yp(1) β*y(1)*y(2)-γ*y(2)-yp(2) y(1)+y(2)+y(3)-1]; end y20 = 1e-6; β = 0.2; γ = 0.05; p = [β;γ]; y0 = [1-y20; y20; 0]; yp0 = zeros(y0); function sensres=rS_complex(t, y, yp, yS, ypS, p) np = length(p); sensres = zeros(length(y),np); d = 1e-200; id = %i*d; E = eye(np,np) for i=1:length(p) sensres(:,i) = imag(rsir(t,y+id*yS(:,i),yp+id*ypS(:,i),p+id*E(:,i)))/d; end endfunction [t,y,info] = ida(rsir, [0 200], y0, yp0, ... sensPar = [β;γ], ... sensRes = rS_complex, ... yIsAlgebraic=3,... calcIc="y0yp0") clf plot(t',squeeze(info.s(:,2,:))') legend("$\Large\partial "+["y_1","y_2","y_3"]+"/\partial\gamma"+"$")
Options
| sensPar | a double array with the values of parameters w.r.t. which sensitivity is to be computed. |
| sensParIndex | an array of integers between 1 and |
| yS0,ypS0 | The initial condition of the sensitivity function and of its derivtive, i.e. |
| sensRes | a function, a string or a list, the residual of the sensitivity equation. When the right hand side of the DAE is known explicitely and computation of its derivative is tractable (e.g. by symbolic differentiation or by any automatic procedure, including complex step), giving the true residual improves the precision and the computation time. When sensRes is a Scilab function, its prototype must be dsdt = sensRes(t, y, yp, s, sp, p, ...) |
| sensErrCon | By default, sensErrCon is set to %f. If sensErrCon=%t then both state variables and sensitivity variables are included in the error tests. |
| sensCorrStep | "simultaneous" (the default) or "staggered": when sensCorrStep="simultaneous", the state and sensitivity variables are corrected at the same time. If sensCorrStep="staggered", the correction step for the sensitivity variables takes place at the same time for all sensitivity equations, but only after the correction of the state variables has converged and the state variables have passed the local error test. |
| typicalPar | This option serves as positive scaling factors when the right-hand side of the sensitivity is computed by cvode using internal finite difference-quotients. The results will be more accurate if an order of magnitude information is provided. Typically, if no component vanishes, the value of sensPar can be used. |
See also
- arkode — SUNDIALS ordinary differential equation additive Runge-Kutta solver
- cvode — SUNDIALS ordinary differential equation solver
- ida — SUNDIALS differential-algebraic equation solver
- ODE Sensitivity — Forward Sensitivity computation with cvode
- User functions — Coding user functions used by SUNDIALS solvers
- Options (ODE and DAE solvers) — Changing the default behavior of solver
- SUN_Clink — Compiling and linking a C user function
| Report an issue | ||
| << Pure quadrature | Options, features and user functions | Sensitivity (ODE) >> |