cdfbin
fonction de répartition de la distribution binomiale
Séquence d'appel
[P,Q]=cdfbin("PQ",S,Xn,Pr,Ompr) [S]=cdfbin("S",Xn,Pr,Ompr,P,Q) [Xn]=cdfbin("Xn",Pr,Ompr,P,Q,S) [Pr,Ompr]=cdfbin("PrOmpr",P,Q,S,Xn)
Paramètres
- P,Q,S,Xn,Pr,Ompr
six vecteurs réels de même taille.
- P,Q (Q=1-P)
La somme de 0 à S de la distribution (Probabilité de S succès ou moins en XN essais de probabilité de succès PR) En entrée : [0,1].
- S
Le nombre de succès observés En entrée : [0, XN] En recherche : [0, XN]
- Xn
Le nombre d'essais binomiaux En entrée : (0, +infini). En recherche : [1E-300, 1E300]
- Pr,Ompr (Ompr=1-Pr)
La probabilité de succès de chaque essai En entrée : [0,1]. En recherche : [0,1]
Description
Étant donnés les autres, calcule un paramètre de la distribution binomiale
La formule 26.5.24 de Abramowitz et Stegun, Handbook of Mathematical Functions (1966) est utilisée pour réduire le calcul de la fonction de répartition de la distribution à celle d'une loi beta incomplète.
Le calcul des autres paramètres implique une recherche d'une valeur conduisant à la valeur désirée pour P. La recherche dépend de la monotonicité de P par rapport aux autres paramètres.
Tiré de la bibliothèque DCDFLIB: Library of Fortran Routines for Cumulative Distribution Functions, Inverses, and Other Parameters (February, 1994) Barry W. Brown, James Lovato and Kathy Russell. The University of Texas.
Exemples
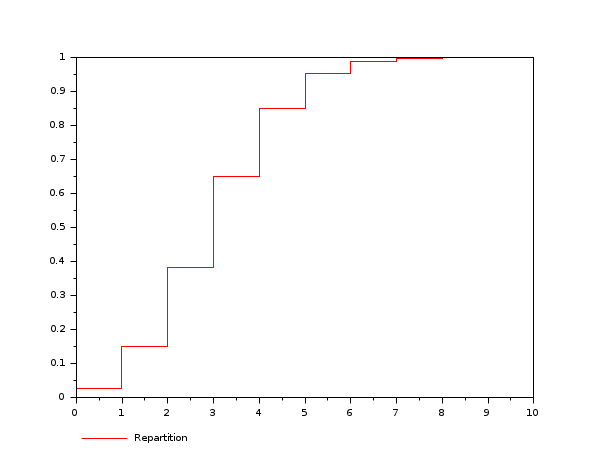
S = 0:1:10; Pr = 0.3 * ones(S); Ompr = 1-Pr; Xn = 10*ones(S); [p,q]=cdfbin('PQ',S,Xn,Pr,Ompr); plot2d2("gnn",[0:10]',p,5,"111","Repartition",[0,0,10,1])
Voir aussi
- cdfbet — fonction de répartition de la distribution Beta
- cdfchi — fonction de répartition de la distribution du chi-deux
- cdfchn — fonction de répartition de la distribution du chi-deux non centrée
- cdff — fonction de répartition de la distribution de Fisher
- cdffnc — fonction de répartition de la distribution de Fisher non centrée
- cdfgam — fonction de répartition de la distribution gamma
- cdfnbn — fonction de répartition de la distribution binomiale négative
- cdfnor — fonction de répartition de la distribution normale
- cdfpoi — fonction de répartition de la distribution de Poisson
- cdft — fonction de répartition de la distribution de Student
| Report an issue | ||
| << cdfbet | Fonctions de répartition | cdfchi >> |