PID
Régulateur PID
Aperçu

Contenu
Description
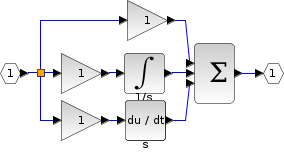
Ce bloc implante un régulateur PID. Le calcul (algorithme) du régulateur PID invoque trois paramètres séparés; Les coefficients d'action Proportionnelle, Intégrale et Dérivée. Le coefficient d'action Proportionnelle détermine la réaction à l'erreur courante. L'intégrale détermine la réaction à la somme des erreurs récentes. Et la Dérivée détermine la réaction à la vitesse à laquelle l'erreur est modifiée. La somme pondérée de ces trois actions est utilisée pour ajuster le processus à travers un élément de contrôle tel que la position d'une vanne de régulation ou l'alimentation de puissance d'un élément chauffant.
Paramètres
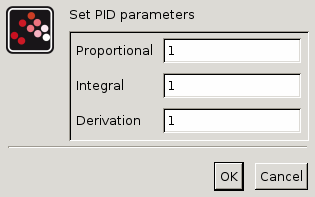
Proportional
La valeur du gain qui multiplie l'erreur.
Propriétés Type 'vec' de taille -1.
Integral
La valeur du temps d'intégration de l'erreur.(1/Integral)
Propriétés Type 'vec' de taille -1.
Derivation
La valeur du temps de dérivation de l'erreur.
Propriétés Type 'vec' de taille -1.
Propriétés par défaut
always active: non
direct-feedthrough: non
zero-crossing: non
mode: non
regular inputs:
- port 1 : size [-1,-2] / type 1
regular outputs:
- port 1 : size [-1,-2] / type 1
number/sizes of activation inputs: 0
number/sizes of activation outputs: 0
continuous-time state: non
discrete-time state: non
object discrete-time state: non
name of computational function: csuper
Fonction d'interfaçage
SCI/modules/scicos_blocks/macros/Linear/PID.sci
Contenu du Superbloc compilé
Exemples
Exemple 1
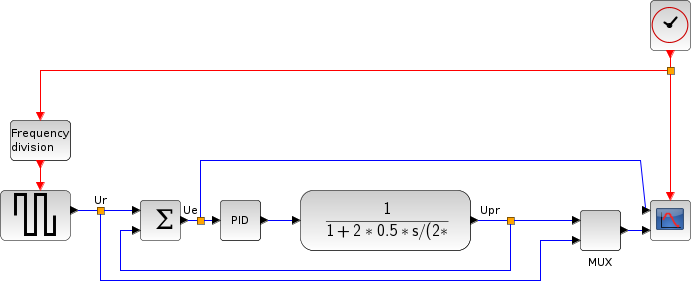
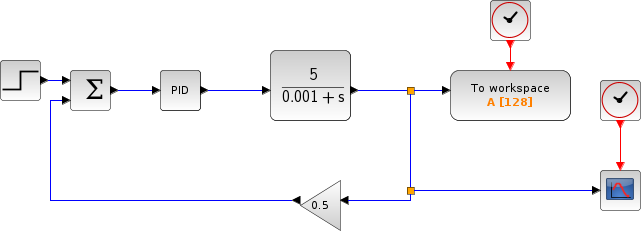
Cet exemple illustre l'utilisation d'une régulation PID. Il permet de faire converger aisément le signal de sortie Upr(t) vers le signal requis Ur(t).
Dans cet exemple, le régulateur est un filtre passe-bas d'ordre 2 et de gain unité, avec un taux d'amortissement ξ=0.5 et une fréquence de coupure fc= 100 Hz. Sa fonction de transfert H(s) est :
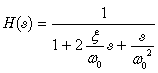
Pour modéliser ce filtre, nous utilisons le bloc de Fonction de transfert continue (CLR) proposé dans la palette Systèmes à temps continu.
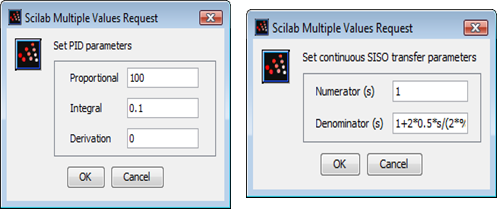
Les paramètres PID Kp, Ki et Kd sont respectivement établis à 100, 0.1 et 0.
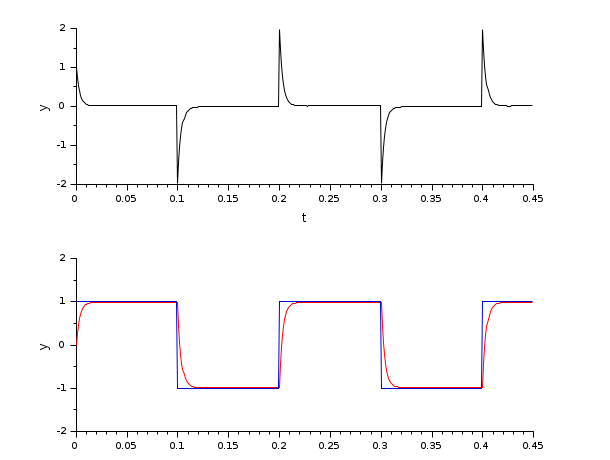
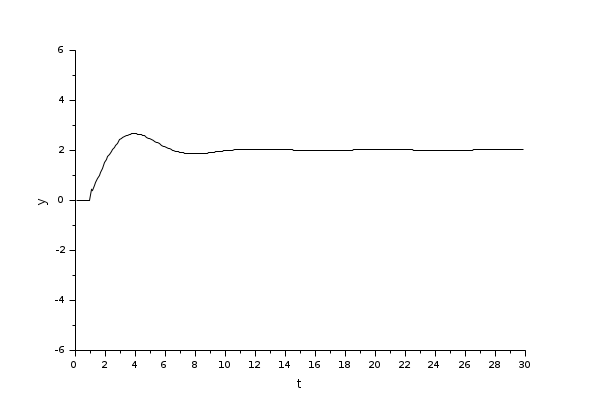
L'oscilloscope affiche la courbe d'erreur (écart à la consigne), Ue (black), le signal de consigne (référence) Ur (bleu), et le signal effectif Upr (rouge). Il montre l'écart initial entre le signal effectif Upr(t) et le signal de consigne Ur(t).
Exemple 2
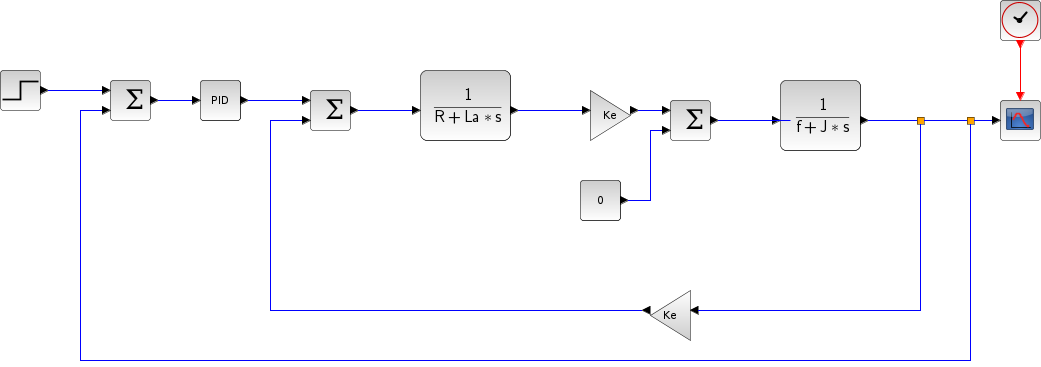
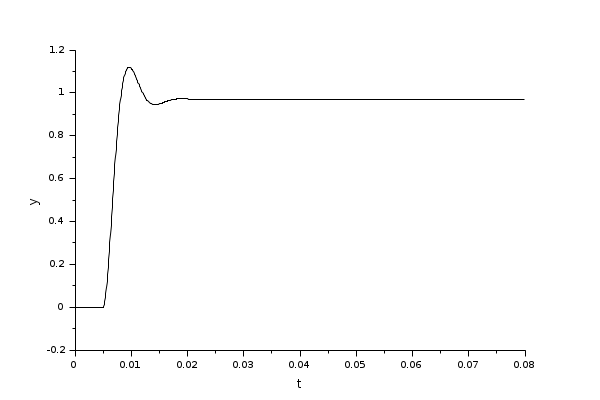
Exemple 3
| Report an issue | ||
| << INTEGRAL_m | Palette Systèmes à temps continu | TCLSS >> |