Comparaisons
Cette page compare les solveurs pour déterminer lequel est le mieux adapté au le problème étudié.
Introduction
Suivant le type de problème, trouver la meilleure méthode n'est pas toujours évident, on ne peut que tirer des règles générales. C'est de celles-ci que l'on parle dans cette page.
Pas Fixe et pas Variable
Les solveurs sont divisés en deux familles principales : celles à pas variable et celles à pas fixes.
Dans les méthodes à pas variable, le pas de temps peut varier suivant la dynamique du modèle et les tolérances.
S'il recherche un temps de simulation stable, l'utilisateur doit sélectionner un solveur à pas fixe, parce-que le temps de calcul du nouveau pas d'un solveur à pas variable ne peut pas être prédit correctement.
Bien que pour un problème simple (ou hautes tolérances), un solveur à pas variable peut diminuer le temps de simulation en calculant de grands pas, un solveur à aps fixe est préférable si le pas de temps idéal est connu et à peu près constant (l'utilisateur peut alors le renseigner dans max step size).
Pas Variable:
- LSodar
- CVode
- IDA
- Runge-Kutta 4(5)
- Dormand-Prince 4(5)
- Runge-Kutta Implicite 4(5)
- Crank-Nicolson 2(3)
Les solveurs d'EDO à pas variable ne sont pas appropriés pour des applications temps réel déterministes car le surplus de calcul au passage d'un pas de temps varie au cours de l'application.
Explicite et Implicite - Raideur
A l'intérieur de ces deux familles, on peut distinguer les solveurs Explicites des Implicites.
Alors que les méthodes explicites n'utilisent que des informations du pas actuel, les implicites tentent d'estimer les dérivées à des temps futurs. Pour faire cela, elles utilisentdes solveurs non linéaires telle que itérations point-fixe, itérations fonctionnelles (non-raide) ou Newton modifiées (raide).
Le choix de la famille est habituellement déterminé par la raideur du problème, qui estquand il y a une différence importante entre les modules des valeurs propres extrêmesde la matrice jacobienne (mal conditionnée). C'est généralement un système sensible aux discontinuités, en cela que la précision requise n'est pas constante.
Implicites:
- LSodar
- CVode
- IDA
- Runge-Kutta Implicite 4(5)
- Crank-Nicolson 2(3)
- Runge-Kutta 4(5)
- Dormand-Prince 4(5)
En un mot, les Explicites calculent directement la solution, alors que les Implicites se concentrent sur la stabilité, impliquant plus d'opérations, suivant les tolérances.
Alors comment choisir ?
Puisqu'il n'est pas possible de savoir avec certitude si tel solveur sera efficace sur un système donné, le meilleur moyen est de lancer le plus probable et de comparer les résultats avec les autres.
L'utilisateur doit d'abord établir la compexité de son problème (stabilité / raideur) et s'il désire une grande précision, une simulation rapide, un temps prévisible ou un programme automatisé.
Précision : CVode,
Temps prévisible : Pas Fixe.
Temps de simulation : LSodar,
Automatisé : LSodar,
Exemples - ODEs
Commençons par un exemple non-raide simple : une intégration de Sinus.
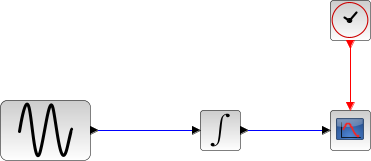
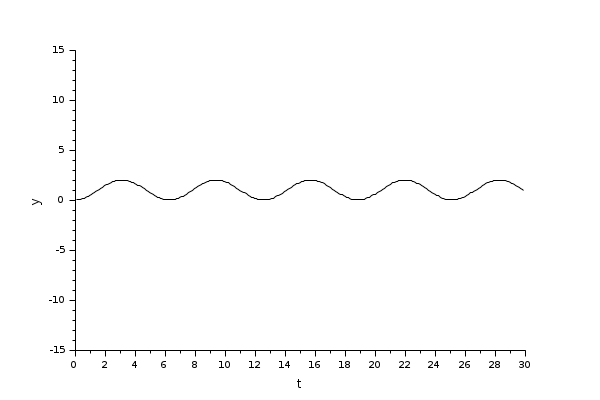
Dans le script suivant, on compare la différence de temps entre les solveurs en lançant l'exemple avec différents solveurs tour à tour (IDA n'est pas adapté à ce genre de problème) : Ouverture du script
La console Scilab affiche :
Temps pour LSodar :
10.1
Temps pour CVode BDF/Newton :
31
Temps pour CVode BDF/Functional :
30
Temps pour CVode Adams/Newton :
17.211
Temps pour CVode Adams/Functional :
16.305
Temps pour Dormand-Prince :
12.92
Temps pour Runge-Kutta :
7.663
Temps pour Runge-Kutta implicite :
10.881
Temps pour Crank-Nicolson :
7.856
Ces résultats montrent que pour un problème non-raide simple et à même précision, Runge-Kutta est le plus rapide.
En dépit du calcul de nouveau pas de temps, LSodar n'est pas très éloigné des solveurs à pas fixe solvers parce-qu'il détermine de larges pas de temps.
Des résultats, on peut extraire des facteurs de vitesse et dresser le tableau suivant :
| BDF / Newton | BDF / Functional | Adams / Newton | Adams / Functional | Dormand-Prince | Runge-Kutta | Runge-Kutta Implicite | Crank-Nicolson | |
| LSodar | 3.1x | 3x | 1.7x | 1.6x | 1.3x | 0.75x | 1.08x | .07x |
| BDF / Newton | 0.1x | 0.6x | 0.5x | 0.4x | 0.25x | 0.35x | 0.23x | |
| BDF / Functional | 0.6x | 0.5x | 0.4x | 0.25x | 0.4x | 0.24x | ||
| Adams / Newton | 0.9x | 0.75x | 0.45x | 0.6x | 0.42x | |||
| Adams / Functional | 0.8x | 0.5x | 0.7x | 0.45x | ||||
| Dormand-Prince | 0.6x | 0.8x | 0.56x | |||||
| Runge-Kutta | 1.4x | 0.95x | ||||||
| Runge-Kutta Implicite | 0.67x |
Ensuite, un contrôleur basique à six états continus est testé.
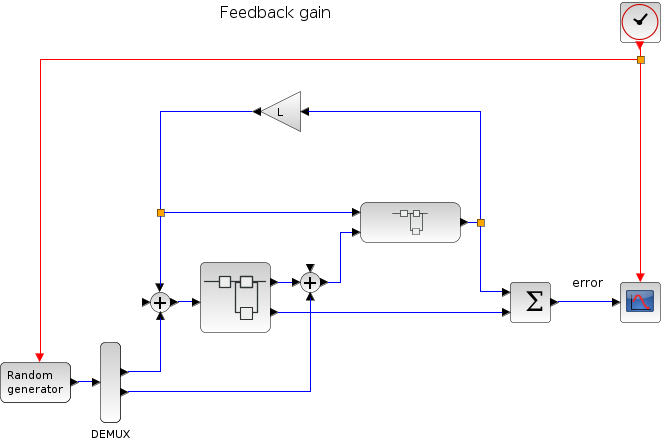

Dans le script suivant, on compare la différence de temps entre les solveurs en lançant l'exemple avec les neuf solveurs tout à tour (IDA n'est pas adapté à ce genre de problème) : Ouverture du script
La console Scilab affiche :
Temps pour LSodar :
10
Temps pour CVode BDF/Newton :
28.254
Temps pour CVode BDF/Functional :
25.545
Temps pour CVode Adams/Newton :
15
Temps pour CVode Adams/Functional :
12.1
Temps pour Dormand-Prince :
2.359
Temps pour Runge-Kutta :
1.671
Temps pour Runge-Kutta implicite :
5.612
Temps pour Crank-Nicolson :
3.345
Ces résultats montrent que quand la raideur apparaît légèrement, BDF / Newton commence à prendre de la vitesse. Mais le problème n'est pas encore suffisamment compliqué pour que cette méthode soit intéressante.
Le tableau des facteurs de vitesse :
| BDF / Newton | BDF / Functional | Adams / Newton | Adams / Functional | Dormand-Prince | Runge-Kutta | Runge-Kutta Implicite | Crank-Nicolson | |
| LSodar | 2.8x | 2.6x | 1.5x | 1.2x | 0.2x | 0.17x | 0.5x | 0.33x |
| BDF / Newton | 0.9x | 0.5x | 0.4x | 0.1x | 0.05x | 0.2x | 0.12x | |
| BDF / Functional | 0.6x | 0.5x | 0.1x | 0.07x | 0.2x | 0.13x | ||
| Adams / Newton | 0.8x | 0.15x | 0.1x | 0.4x | 0.22x | |||
| Adams / Functional | 0.2x | 0.1x | 0.5x | 0.28x | ||||
| Dormand-Prince | 0.7x | 2.4x | 1.42x | |||||
| Runge-Kutta | 3.4x | 2x | ||||||
| Implicit Runge-Kutta | 0.6x |
A présent, on utilise le filtre de Kalman, contenant quinze états continus.
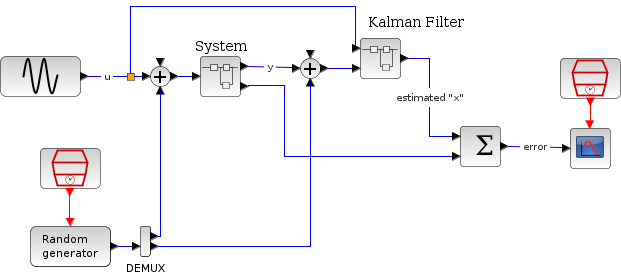

Dans le script suivant, on compare la différence de temps entre les solveurs en lançant l'exemple avec les neuf solveurs tout à tour (IDA n'est pas adapté à ce genre de problème) : Ouverture du script
La console Scilab affiche :
Temps pour LSodar :
10
Temps pour CVode BDF/Newton :
21.3
Temps pour CVode BDF/Functional :
15.8
Temps pour CVode Adams/Newton :
12.5
Temps pour CVode Adams/Functional :
8.67
Temps pour Dormand-Prince :
1.244
Temps pour Runge-Kutta :
0.87
Temps pour Runge-Kutta implicite :
4
Temps pour Crank-Nicolson :
2.657
Ces résultats indiquent que pour un problème pour conséquent (plus d'états continus implique plus d'équations), les itérations de Newton commencent à montrer de l'intérêt, elles se rapprochent des autres solveurs.
Le tableau des facteurs de vitesse :
| BDF / Newton | BDF / Functional | Adams / Newton | Adams / Functional | Dormand-Prince | Runge-Kutta | Runge-Kutta Implicite | Crank-Nicolson | |
| LSodar | 2.1x | 1.6x | 1.3x | 0.85x | 0.1x | 0.1x | 0.4x | 0.26x |
| BDF / Newton | 0.75x | 0.6x | 0.4x | 0.06x | 0.05x | 0.2x | 0.12x | |
| BDF / Functional | 0.8x | 0.55x | 0.08x | 0.06x | 0.25x | 0.17x | ||
| Adams / Newton | 0.7x | 0.1x | 0.07x | 0.3x | 0.21x | |||
| Adams / Functional | 0.15x | 0.1x | 0.5x | 0.3x | ||||
| Dormand-Prince | 0.7x | 3.2x | 2.1x | |||||
| Runge-Kutta | 4.6x | 3.1x | ||||||
| Implicit Runge-Kutta | 0.66x |
Exemples - EDAs
Dans cette section, on compare IDA à DDaskr.
Exemple : une balle rebondissante.
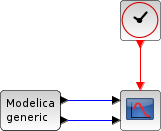
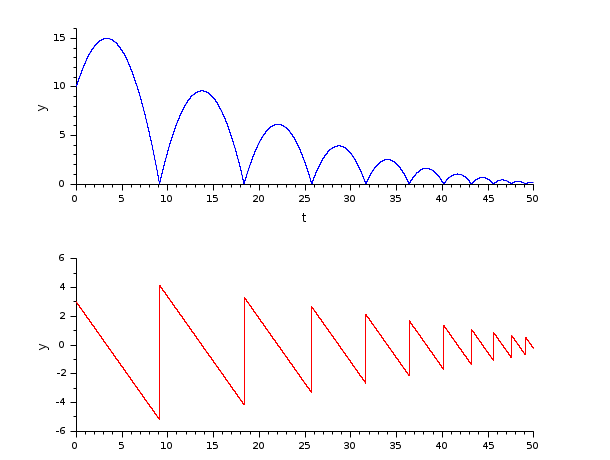
Dans le script suivant, on compare la différence de temps entre les solveurs en lançant les trois solveurs tout à tour : Ouverture du script
La console Scilab affiche :
Temps pour IDA :
7.5
Temps pour DDaskr - Newton :
5.4
Temps pour DDaskr - GMRes :
10.2
Ces résultats montrent que pour un problème raide, avec traversées de zéro et à même précision, DDaskr - Newton est le plus rapide.
La différence de temps est attribuée à l'implémentation optimale de DDaskr et à son moindre contrôle d'erreur.
GMRes est plus lent dû à la petitesse du problème (pas suffisamment d'états continus).
Des résultats on extrait les facteurs de vitesse :
| IDA | DDaskr G | |
| DDaskr N | 1.39x | 1.9x |
L'exemple suivant corrobore le précédent, il est plus court mais plus complet, parce-qu'il traite du remplissage et vidage d'une cuve.
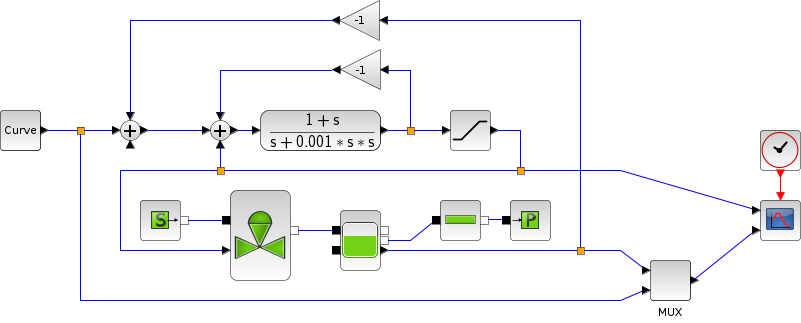
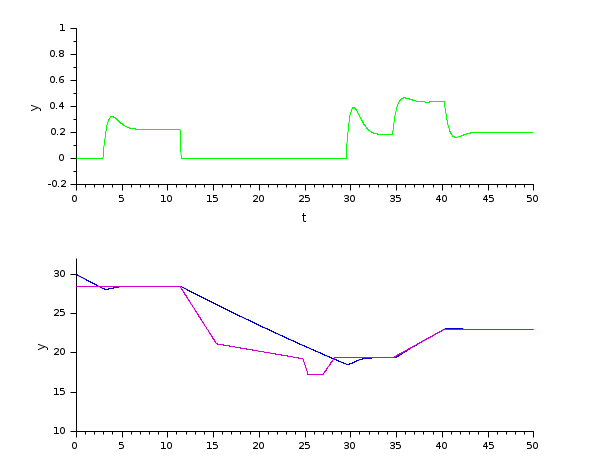
Dans le script suivant, on compare la différence de temps entre les solveurs en lançant les trois solveurs tout à tour: Ouverture du script
La console Scilab affiche :
Temps pour IDA :
3
Temps pour DDaskr - Newton :
0.8
Temps pour DDaskr - GMRes :
0.85
Des résultats on extrait les facteurs de vitesse :
| IDA | DDaskr G | |
| DDaskr N | 3.75x | 1.06x |
Voir Aussi
- LSodar — LSodar (abréviation de "Livermore Solver for Ordinary Differential equations, with Automatic method switching for stiff and nonstiff problems, and with Root-finding") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinaires (EDOs).
- CVode — CVode (abréviation de "C-language Variable-coefficients ODE solver") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs). Il utilise BDF ou Adams comme méthode d'intégration, et des itérations fonctionnelles ou de Newton.
- IDA — "Implicit Differential Algebraic equations system solver" est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Algebriques (EDAs).
- Runge-Kutta 4(5) — Runge-Kutta est un solveur numérique fournissant une méthode explicite efficace pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs).
- Dormand-Prince 4(5) — Dormand-Prince est un solveur numérique fournissant une méthode explicite efficace pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs).
- Runge-Kutta Implicite 4(5) — Solveur numérique fournissant une méthode implicite efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs)
- Crank-Nicolson 2(3) — Crank-Nicolson est un solveur numérique basé sur le schéma Runge-Kutta fournissant une méthode implicite efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinaires (EDOs). Appelé par xcos.
- DDaskr — "Double-precision Differential Algebraic equations system Solver with Krylov method and Rootfinding" : solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Algebriques (EDAs).
- ode — solveur d'équations différentielles ordinaires
- ode_discrete — ordinary differential equation solver, discrete time simulation
- ode_root — ordinary differential equation solver with roots finding
- odedc — discrete/continuous ode solver
- impl — differential algebraic equation
| Report an issue | ||
| << Recherche de racines | Solveurs | xcos >> |