Scilab Website | Contribute with GitLab | Mailing list archives | ATOMS toolboxes
Scilab Online Help
2024.0.0 - English


xcov

Computes discrete auto or cross covariance

Syntax

[c, lagindex] = xcov(x)
[c, lagindex] = xcov(x, y)
[c, lagindex] = xcov(.., maxlags)
[c, lagindex] = xcov(.., maxlags, scaling)

Parameters

x

a vector of real or complex floating point numbers.

y

a vector of real or complex floating point numbers. The default value is x.

maxlags

a scalar with integer value greater than 1. The default value is n. Where n is the maximum of the x and y vector length.

scaling

a character string with possible value: "biased", "unbiased", "coeff", "none". The default value is "none".

c

a vector of real or complex floating point numbers with same orientation as x.

lagindex

a row vector, containing the lags index corresponding to the c values.

Description

  • c=xcov(x) computes the un-normalized discrete covariance:

    {\begin{matrix}C_k = \sum_{i=0}^{n-k-1} {(x_{i+k}-\mu_x})({x_i-\mu_x})^{*} , k \geq 0 \mu_x=\sum_{i=0}^{n-1}{x_i} C_k = C^{*}_{-k}, k \leq -1\end{matrix}.}$

    and return in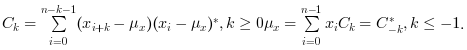 c the sequence of covariance lags Ck=-n:n where n is the length of x
  • xcov(x,y) computes the un-normalized discrete cross covariance:

    ${\begin{matrix}C_k = \sum_{i=1}^{n-k} {(x_{i+k}-\mu_x})*({y_i}-\mu_y)^{*}, k \geq 0 \mu_x=\sum_{i=0}^{n-1}{x_i} \mu_y=\sum_{i=0}^{n-1}{y_i} C_k = C^{*}_{-k}, k \leq -1\end{matrix}.}$

    and return in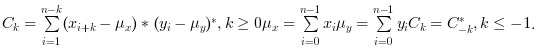 c the sequence of cross covariance lags Ck=-n:n where n is the maximum of x and y length's.

If the maxlags argument is given xcov returns in c the sequence of covariance lags Ck=-maxlags:maxlags. If maxlags is greater than length(x), the first and last values of c are zero.

The scaling argument describes how C(k) is normalized before being returned in c:

  • "biased": c=C/n.
  • "unbiased": c=C./(n-(-maxlags:maxlags)).
  • "coeff": c=C/(norm(x)*norm(y)).

Remark

The corr function computes the "biased" covariance of x and y and only return in c the sequence of covariance lags Ck≥0 .

Method

This function computes C using xcorr(x-mean(x),y-mean(y),...).

Examples

t = linspace(0, 100, 2000);
y = 0.8 * sin(t) + 0.8 * sin(2 * t);
[c, ind] = xcov(y, "biased");
plot(ind, c)

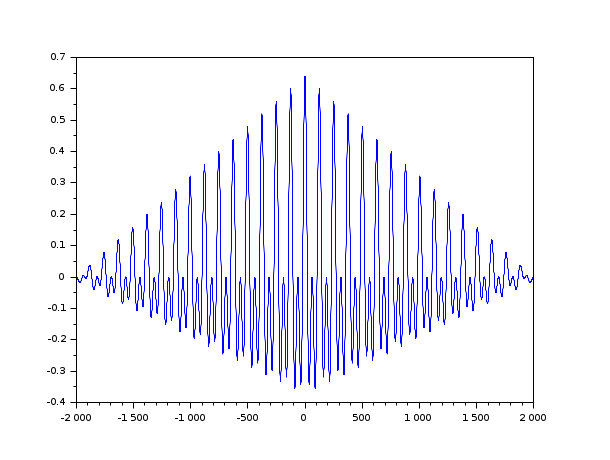
See also

  • xcorr — Computes discrete auto or cross correlation
  • corr — correlation, covariance
  • fft — Direct or inverse Fast Fourier Transform of a vector, matrix, or hypermatrix

History

VersionDescription
5.4.0 xcov added.
Report an issue
<< unwrap Signal Processing FFTW >>
Copyright (c) 2022-2024 (Dassault Systèmes)
Copyright (c) 2017-2022 (ESI Group)
Copyright (c) 2011-2017 (Scilab Enterprises)
Copyright (c) 1989-2012 (INRIA)
Copyright (c) 1989-2007 (ENPC)
with contributors 		Last updated:
Tue Oct 24 14:30:04 CEST 2023