factorial
функция факториала : произведение первых n положительных целых чисел
Синтаксис
f = factorial(n) [f, p] = factorial(n) [f, p, m] = factorial(n)
Аргументы
- n
скаляр, вектор, матрица или гиперматрица положительных целых чисел <= 1014.
- f
массив чисел типа double того же размера, что и
n:f(i) = n(i)!. Значенияfмогут быть вплоть доn=21.- p
массив чисел типа double того же размера, что и
n: 10 в степениf:p(i) = int(log10(f(i)!)).- m
массив чисел типа double в интервале
[1,10)того же размера, что иn: мантисса уfтакая, чтоn(i)! = m(i) * 10^p(i).
Описание
Возвращает факториал от n, равный произведению 1 * 2 * ... * n.
 | f превышает разрядную сетку при n>170 и всегда возвращает %inf для любого большего n. |
 |
|
Граф
Примеры
Таблица первых точных значений факториала n! :
--> [n factorial(n)] ans = 0. 1. 1. 1. 2. 2. 3. 6. 4. 24. 5. 120. 6. 720. 7. 5040. 8. 40320. 9. 362880. 10. 3628800. 11. 39916800. 12. 479001600. 13. 6227020800. 14. 87178291200. 15. 1307674368000. 16. 20922789888000. 17. 355687428096000. 18. 6402373705728000. 19. 121645100408832000. 20. 2432902008176640000. 21. 51090942171709440000.
Округление значения factorial() в большую сторону в представлении с плавающей запятой:
factorial(170) // 7.257415615307998967e306 factorial(171) // %inf
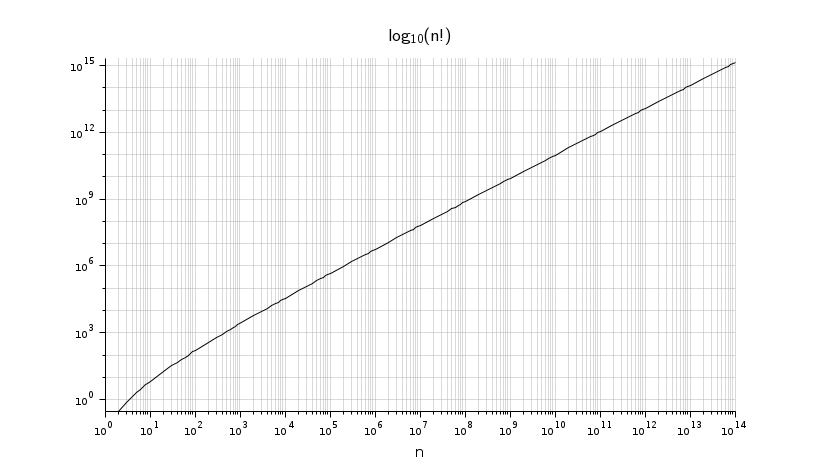
Построение графика функции во всём её интервале:
x = (10^(0:13)).*.(1:9); x(1)=[]; x($)=1e14; [f, p, m] = factorial(x); clf plot2d("ll", x, p+log10(m)) xlabel("n", "fontsize",3) title("$\mathsf{log_{10}(n!)}$", "fontsize", 4) xgrid(color("grey70"), 1, 7) set(gca(), "sub_ticks",[8 2], "tight_limits","on"); gca().data_bounds([1 4]) = [1 2e15]; gcf().axes_size = [850 480];
Относительные ошибки factorial():
n = 10^(1:14)'; [f, p, m] = factorial(n); // Точная (ограниченная) мантисса для n = 10^(1:14) : m0 = [ 3.6288000000000000 9.3326215443944153 4.0238726007709377 .. // n = 10 100 1000 2.8462596809170545 2.8242294079603479 .. // n = 10000 100000 8.2639316883312401 1.2024233400515904 1.6172037949214624 .. // n = 1e6 1e7 1e8 9.9046265792229937 2.3257962056730834 3.7489285991050270 .. // n = 1e9 1e10 1e11 1.4036611603737561 2.4033300843401153 1.6456020559872979 // n = 1e12 1e13 1e14 ]'; r_err = m./m0 - 1; [n r_err]
--> [n r_err] ans = 10. 0. 100. -5.551D-16 1000. 1.132D-13 10000. 1.918D-12 100000. 6.611D-12 1000000. 9.962D-11 10000000. 5.048D-08 100000000. 1.050D-08 1.000D+09 0.0000001 1.000D+10 0.0000019 1.000D+11 0.0000062 1.000D+12 0.0001327 1.000D+13 0.0004839 1.000D+14 0.0071116
Смотрите также
История
| Версия | Описание |
| 6.1 | Расширение вплоть до n = 1014.
Добавлено p в 10-й степени и вывод мантиссы m. |
| Report an issue | ||
| << factor | Дискретная математика | gcd >> |