qpsolve
線形二次計画ソルバー
呼び出し手順
[x [,iact [,iter [,f]]]]=qpsolve(Q,p,C,b,ci,cs,me)
パラメータ
- Q
実数正定対称行列 (次元
n x n).- p
実数 (列) ベクトル (次元
n)- C
実数行列 (次元
(me + md) x n). この行列は通常行列または疎行列とすることができます.- b
RHS 列ベクトル (次元
m=(me + md))- ci
下限の列ベクトル (次元
n). 下限に関する制約がない場合,ci = []としてください.xの何らかの要素に 下界が存在する場合,ciの他の(拘束されていない)値を 非常に大きな負の値(例えば,ci(j) = -number_properties('huge'))に設定してください.- cs
上限の列ベクトル. (上記の注意と同じ).
- me
等式拘束の数 (すなわち
C(1:me,:)*x = b(1:me))- x
見つかった最適解.
- iact
ベクトル, アクティブな拘束のインジケータ. 最初の非ゼロのエントリはアクティブな拘束のインデックスとなります
- iter
2x1ベクトル, 最初の要素には "main" 反復の数を出力します. 2番目の要素には,アクティブになった後に削除された拘束の数を出力します.
説明
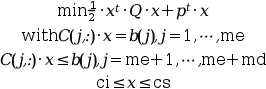
この関数は,Qが対称正定であることを必要とします.
この仮定が満たされない場合には, Scilab quaproツールボックスで
指定されたquapro 関数を使用することができます.
qpsolveソルバーは, コンパイルされたqp_solveプリミティブをコールする Scilabスクリプトとして実装されています. この関数は,以前のquaproソルバーを直接置き換えるための 機能として適用されています : つまり, qpsolveソルバーは 同じインターフェイスを提供する, 同じ入出力引数を有するように設計されています. しかし,入力引数x0 と impがquaproでは利用可能ですが, qpsolveは利用できません.
例
//以下のような x ( R^6)を探す: //C1*x = b1 (3 個の等式拘束 すなわち me=3) C1= [1,-1,1,0,3,1; -1,0,-3,-4,5,6; 2,5,3,0,1,0]; b1=[1;2;3]; //C2*x <= b2 (2 個の不等式拘束) C2=[0,1,0,1,2,-1; -1,0,2,1,1,0]; b2=[-1;2.5]; // xはciおよびcsの間: ci=[-1000;-10000;0;-1000;-1000;-1000]; cs=[10000;100;1.5;100;100;1000]; // 以下の条件のもとで 0.5*x'*Q*x + p'*x を最小化 p=[1;2;3;4;5;6]; Q=eye(6,6); //初期値を指定しない; C=[C1;C2]; b=[b1;b2]; me=3; [x,iact,iter,f]=qpsolve(Q,p,C,b,ci,cs,me) // 線形拘束 (1 から 4) のみアクティブ
参照
- optim — non-linear optimization routine
- qp_solve — 組み込みの線形二次計画ソルバー
- qld — linear quadratic programming solver
ツールボックス "quapro" も特にQが
特異な場合には有用かもしれません.
参考文献
Goldfarb, D. and Idnani, A. (1982). "Dual and Primal-Dual Methods for Solving Strictly Convex Quadratic Programs", in J.P. Hennart (ed.), Numerical Analysis, Proceedings, Cocoyoc, Mexico 1981, Vol. 909 of Lecture Notes in Mathematics, Springer-Verlag, Berlin, pp. 226-239.
Goldfarb, D. and Idnani, A. (1983). "A numerically stable dual method for solving strictly convex quadratic programs", Mathematical Programming 27: 1-33.
QuadProg (Quadratic Programming Routines), Berwin A Turlach,http://www.maths.uwa.edu.au/~berwin/software/quadprog.html
使用される関数
Goldfarb/Idnani アルゴリズムに基づきBerwin A. Turlach により開発されたqpgen1.f (または QP.solve.f)
| Report an issue | ||
| << qp_solve | Optimization and Simulation | readmps >> |