dsearch
répartit, localise et compte les éléments d'une matrice en catégories données
Séquence d'appel
[i_bin [,counts [,outside]]] = dsearch(X, bins ) [i_bin [,counts [,outside]]] = dsearch(X, bins , pm )
Paramètres
- X
matrice ou hypermatrice de nombres réels, d'entiers encodés, ou de textes : éléments à catégoriser. Les nombres complexes et les polynômes ne sont pas admis.
- bins
vecteur ligne ou colonne définissant les catégories, de même type que
X(SiXcontient des entiers encodés,binspeut être de type décimal).- Cas discret (pm="d"):
binscontient les valeurs auxquelles les éléments deXdoivent être identifiés. SiXest numérique (nombres réels ou entiers encodés),binsdoit être préalablement trié par ordre croissant, et sans doublons. - Cas continu (par défaut, pm="c"):
binscontient les bornes d'intervallesIkcontigus :I1 = [bins(1), bins(2)],I2 = (bins(2), bins(3)],...,In = (bins(n), bins(n+1)]. Noter queI1est fermé à gauche, alors que lesI(k>1)sont semi-ouverts à gauche. Les bornesbinsdoivent être préalablement triées en ordre strictement croissant : bins(1) < bins(2) < ... < bins(n). Pour le traitement du texte, l'ordre lexicographique sensible à la casse est considéré.
- Cas discret (pm="d"):
- pm
"c" (continu, par défaut) ou "d" (discrêt): mode de traitement. En mode continu,
binsspécifie les bornes d'intervalles contigus définissant les catégories à considérer. En mode discrêt,binsfournit les valeurs auxquelles les éléments deXdoivent être individuellement identifiés.- i_bin
Matrice ou hypermatrice de mêmes tailles que
X:i_bin(k)donne le n° de la catégorie à laquelleX(k)appartient. SiX(k)n'appartient à aucune catégorie,i_bin(k) = 0.- counts
- Nombre d'éléments de X dans les catégories respectives.
Cas continu(pm="c"): counts(i) éléments de
Xappartiennent à l'intervalleIktel que défini ci-dessus (voir le paramètrebins). Les éléments deXjuste égaux à bins(1) sont comptés dans counts(1).countsest un vecteur de même taille quebins, - 1.Cas discrêt(pm="d"):
counts(i)indique le nombre d'éléments deXégaux àbins(i) - outside
Nombre total d'éléments de X n'appartenant à aucune catégorie
bins.
Description
Pour chaque élément X(i), la fonction dsearch détermine la valeur bins(j) ou l'intervalle (bins(j), bins(j+1)] égale à ou contenant X(i). Elle retourne i_bin(i) = j, ou 0 si aucune valeur ou intervalle ne convient (le premier intervalle inclut bins(1) à gauche). L'effectif de chaque de chaque catégorie est retourné dans le vecteur counts. Le nombre d'éléments de X n'allant dans aucune catégorie est retourné dans outside (donc outside = sum(bool2s(i_bin==0))).
dsearch(..) peut être surchargée.
Le mode pm="c" par défaut peut être utilisé pour calculer l'histogramme empirique d'une fonction appliquée à un ensemble de points donnés.
Exemples
// TEXTES en valeurs PARTICULIERES // ------------------------------- i = grand(4,6,"uin",0,7)+97; T = matrix(strsplit(ascii(i),1:length(i)-1), size(i)); T(T=="f") = "#"; T(T=="a") = "AA"; T bins = [ strsplit(ascii(97+(7:-1:0)),1:7)' "AA"] [i_bin, counts, outside] = dsearch(T, bins, "d") // TEXTES categorisés par INTERVALLES LEXICOGRAPHIQUES // --------------------------------------------------- // Génération d'une matrice texte aléatoire nL = 3; nC = 5; L = 3; s = ascii(grand(1,nL*nC*L,"uin",0,25)+97); T = matrix(strsplit(s, L:L:nL*nC*L-1), nL, nC); // Génération d'intervalles lexicographiques aléatoires ordonnés L = 2; nC = 6; s = ascii(grand(1,nC*L,"uin",0,25)+97); bins = unique(matrix(strsplit(s, L:L:nC*L-1), 1, nC)) T [i_bin, counts, outside] = dsearch(T, bins)
Dans l'exemple suivant, considérons 3 intervalles I1 = [5,11],
I2 = (11,15] and I3 = (15,20].
Nous recherchons les n° des intervalles respectifs auxquels les éléments de X = [11 13 1 7 5 2 9] appartiennent.
[i_bin, counts, outside] = dsearch([11 13 1 7 5 2 9], [5 11 15 20])
Résultat affiché :
-->[i_bin, counts, outside] = dsearch([11 13 1 7 5 2 9], [5 11 15 20])
outside =
2.
counts =
4. 1. 0.
i_bin =
1. 2. 0. 1. 1. 0. 1.
En effet,
X(1)=11 est dans l'intervalle I1, donc i_bin(1)=1.
X(2)=13 est dans l'intervalle I2, donc i_bin(2)=2.
X(3)=1 n'appartient à aucun des intervalles définis, donc i_bin(3)=0.
X(4)=7 est dans l'intervalle I1, donc i_bin(4)=1.
...
4 éléments de X (5, 7, 9 et 11) appartiennent à I1, donc counts(1)=4.
Seul un élément de X (13) est dans I2, donc counts(2)=1.
Aucun élément de X est dans I3, donc counts(3)=0.
Deux éléments de X (i.e. 1, 2) n'appartiennent à aucun intervalle défini, donc outside=2.
// Nombres à identifier à des valeurs discrêtes // -------------------------------------------- [i_bin, counts, outside] = dsearch([11 13 1 7 5 2 9], [5 11 15 20],"d" )
affiche
-->[i_bin, counts, outside] = dsearch([11 13 1 7 5 2 9], [5 11 15 20], "d" )
outside =
5.
counts =
1. 1. 0. 0.
i_bin =
2. 0. 0. 0. 1. 0. 0.
En effet,
X(1)=11égalebins(2), donci_bin(1)=2.X(2)=13ne correspond à aucune des valeurs debins, donci_bin(2)=0....
X(7)=9ne correspond à aucune des valeurs debins, donci_bin(7)=0.Un seul élément de X vaut
bin(1)=5, donccounts(1)=1.Aucun élément de X ne vaut
bins(4)=20, donccounts(4)=0.5 éléments de X (i.e. 13, 1, 7, 2, 9) ne sont identiables à aucun des éléments de
bins, doncoutside=5.
Les nombres dans bins doivent être rangés par ordre strictement croissant, que le mode de traitement soit continu ou discrêt. Dans le cas contraire, une erreur se produit.
-->dsearch([11 13 1 7 5 2 9], [2 1])
!--error 999
dsearch : the array s (arg 2) is not well ordered
-->dsearch([11 13 1 7 5 2 9], [2 1],"d")
!--error 999
dsearch : the array s (arg 2) is not well ordered
Exemples avancés
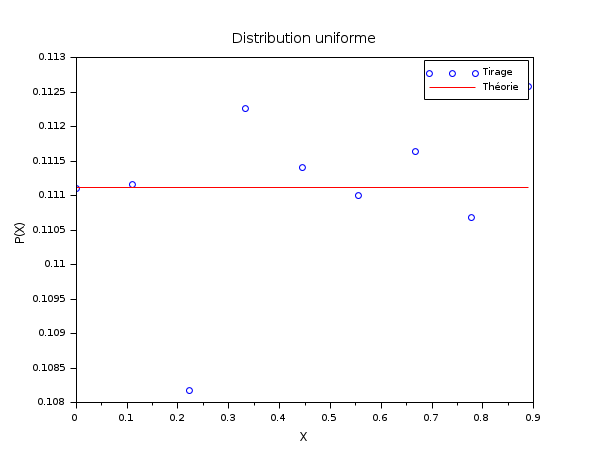
Dans l'exemple suivant, l'histogramme empirique d'un tirage aléatoire à distribution uniforme sur [0, 1] est comparé avec la fonction de distribution théorique uniforme. A cette fin, une catégorisation par intervalles contigus est utilisée (pm="c"). Une matrice X de m=50000 nombres aléatoires à ditribution uniforme sur [0,1[ sont générés. n=10 bornes régulièrement espacées sur [0,1] sont générées et partionnent ce domaine en n-1=9 intervalles de largeurs identiques. dsearch() classe et dénombre les effectifs de X dans chaque intervalle. La valeur de counts(i)/m attendue (pour m -> inf) vaut 1/(n-1).
m = 50000 ; n = 10; X = grand(m,1,"def"); bins = linspace(0,1,n)'; [i_bin, counts] = dsearch(X, bins); e = 1/(n-1)*ones(1,n-1); scf() ; plot(bins(1:n-1), counts/m,"bo"); plot(bins(1:n-1), e',"r-"); legend(["Experiment","Expectation"]); xtitle("Uniform random numbers","X","P(X)");
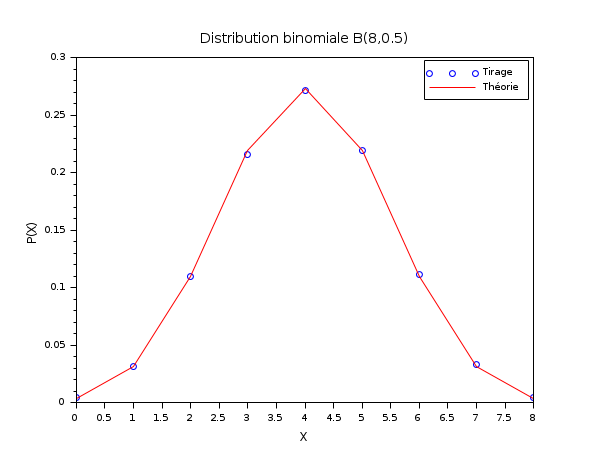
Dans l'exemple suivant, l'histogramme d'un tirage aléatoire à distribution binomiale est comparé avec la fonction de distribution de probabilité binomiale théorique B(N,p), avec N=8 et p=0.5. A cette fin, dsearch() est utilisée en mode discret ("pm="d").
N = 8 ; p = 0.5; m = 50000; X = grand(m,1,"bin",N,p); bins = (0:N)'; [i_bin, counts] = dsearch(X, bins, "d"); Pexp = counts/m; Pexa = binomial(p,N); scf() ; plot(bins, Pexp, "bo"); plot(bins, Pexa', "r-"); xtitle("Distribution binomiale B(8,0.5)","X","P(X)"); legend(["Tirage","Théorie"]);
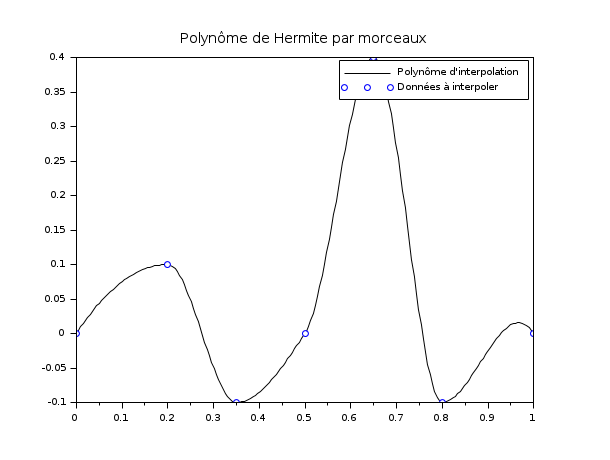
Autre exemple : utilisons maintenant une série de polynômes de Hermite définis par morceaux pour interpoler un ensemble depoints.
// Définition de la base des fonctions de Hermite : function y=Ll(t, k, x) // Lagrange left on Ik y=(t-x(k+1))./(x(k)-x(k+1)) endfunction function y=Lr(t, k, x) // Lagrange right on Ik y=(t-x(k))./(x(k+1)-x(k)) endfunction function y=Hl(t, k, x) y=(1-2*(t-x(k))./(x(k)-x(k+1))).*Ll(t,k,x).^2 endfunction function y=Hr(t, k, x) y=(1-2*(t-x(k+1))./(x(k+1)-x(k))).*Lr(t,k,x).^2 endfunction function y=Kl(t, k, x) y=(t-x(k)).*Ll(t,k,x).^2 endfunction function y=Kr(t, k, x) y=(t-x(k+1)).*Lr(t,k,x).^2 endfunction x = [0 ; 0.2 ; 0.35 ; 0.5 ; 0.65 ; 0.8 ; 1]; y = [0 ; 0.1 ;-0.1 ; 0 ; 0.4 ;-0.1 ; 0]; d = [1 ; 0 ; 0 ; 1 ; 0 ; 0 ; -1]; X = linspace(0, 1, 200)'; i_bin = dsearch(X, x); // Affichage de la courbe : Y = y(i_bin).*Hl(X,i_bin) + y(i_bin+1).*Hr(X,i_bin) + d(i_bin).*Kl(X,i_bin) + d(i_bin+1).*Kr(X,i_bin); scf(); plot(X,Y,"k-"); plot(x,y,"bo") xtitle("Polynôme de Hermite par morceaux"); legend(["Polynôme d''interpolation","Données à interpoler"]); // NOTE : pour vérifier, décommenter et exécuter la ligne suivante // YY = interp(X,x,y,d); plot2d(X,YY,3,"000")
Voir aussi
Historique
| Version | Description |
| 5.5.0 | Extension aux hypermatrices, aux entiers encodés, et au traitement du texte. |
| Report an issue | ||
| << Chercher et trier | Chercher et trier | find >> |