lattn
正規方程式の反復解
呼び出し手順
[la,lb]=lattn(n,p,cov)
引数
- n
フィルタの最大次数
- p
MA部の次元(一定).
p= -1の場合, アルゴリズムは従来の Levinson反復を使用します.- cov
Rk(d次元過程の場合はd*d行列)を有する行列. 以下のように指定します.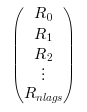
- la
リスト型の変数で, 連続的に計算されたAkを係数とする多項式(1次からn次)を 出力します
説明
以下のシステム (正規方程式)をn(pは固定)について
再帰的に解きます,
つなわち, ARMA(n,p) 過程ベクトルのAR部(極)を同定します.
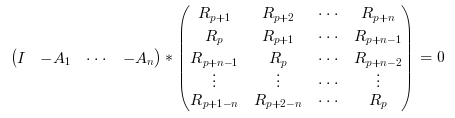
ただし,{Rk;k=1,nlag}
は経験的共分散の系列です.
例
//プロセスを生成 t1=0:0.1:100; y1=sin(2*%pi*t1)+sin(2*%pi*2*t1); y1=y1+rand(y1,"normal"); //Covariance of y1 nlag=128; c1=corr(y1,nlag); c1=c1'; //最大次数=15, p=1 でフィルタ計算 n=15; [la1,sig1]=lattn(n,1,c1); //p=-1,levin関数で極の結果を計算 [la2,sig2]=lattn(n,-1,c1); for i=1:n s2=roots(la2(i)); s2=log(s2)/2/%pi/.1; //推定された極 s2=gsort(imag(s2)); s2=s2(1:i/2); end; [la3,sig3]=levin(n,c1); for i=1:n s3=roots(la3(i)); s3=log(s3)/2/%pi/.1; //推定された極 s3=gsort(imag(s3)); s3=s3(1:i/2); end;
| Report an issue | ||
| << frfit | Identification | lattp >> |