cumsum
sommes partielles cumulatives des éléments d'un tableau.
Séquence d'appel
y = cumsum(x) y = cumsum(x, outtype) y = cumsum(x, orientation) y = cumsum(x, orientation, outtype)
Arguments
- x
tableau de booléens, de nombres entiers, réels, ou complexes, de polynômes, ou de fractions rationnelles. Les hypermatrices ou les matrices booléennes ou numériques creuses sont acceptées.
- orientation
direction selon laquelle les sommes partielles cumulatives sont calculées : Cet argument peut être
le caractère
"*","r","c"ou"m".un nombre entier 1 ≤ orientation ≤ ndims(x) : n° de la dimension selon laquelle les sommes partielles cumulatives directionnelles doivent être calculées. 1 et "r", ou 2 et "c", sont equivalents.
- outtype
mot
"native"ou"double"."double"convertit préalablement en nombres décimaux les booléens ou les entiers fournis.- y
tableau de tailles identiques à celles de
x.
Description
y = cumsum(x) calcule et fournit les sommes partielles
cumulatives y(i)=sum(x(1:i)),
i.e. :
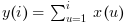
y = cumsum(x, orientation) calcule et fournit dans y les sommes partielles cumulatives des éléments de x selon la direction spécifiée par orientation :
Si orientation est égal à 1 ou "r" alors :
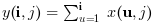 , ou pour un tableau N-Dimensionnel :
, ou pour un tableau N-Dimensionnel :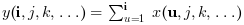
Si orientation est égal à 2 ou "c" alors :
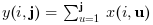 , ou pour un tableau N-Dimensionnel :
, ou pour un tableau N-Dimensionnel :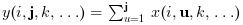
Si orientation est égal à n alors :
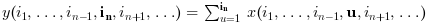
y = cumsum(x,"*") est équivalent à
y = cumsum(x)y = cumsum(x, "m") est équivalent à
y = cumsum(x, orientation), où orientation est le n° de la première dimension de x plus grande que 1. Cette option est utilisé pour compatibilité avec Matlab.
L'argument outtype gère la façon dont le produit est réalisé :
Pour les matrices de nombres décimaux ou complexes, de polynômes, ou de fractions rationnelles, les calculs sont effectués en virgule flottante. Les options
"double"ou"native"sont équivalentes.Pour les tableaux d'entiers,
Par défaut ou si
outtype="native", les calculs sont effectués en arithmétique entière (modulo 2^b, où b est le nombre de bits utilisés).Si
outtype="double", les calculs sont effectués après conversion en nombres décimaux, et les résultats sont fournis en entiers décimaux.Pour les tableaux de booléens,
si
outtype="native", le calcul est effectué sur des booléens (* est remplacée par &),si
outtype="double", le calcul est effectué sur des nombres à virgule flottante (%t est remplacé par 1 et %f par 0).La valeur par défaut est
outtype="double"
 | Lorsque x est une matrice creuse, garder à l'esprit que la densité
de la matrice y résultante sera presque toujours proche de 100%. |
Exemples
Voir aussi
| Report an issue | ||
| << cumprod | Opérations matricielles | kron .*. >> |