convol
convolution
Syntax
y = convol(h, x) [y,e1] = convol(h, x, e0)
Arguments
- h
a vector, first input sequence ("short" one)
- x
a vector, second input sequence ( "long" one)
- e0
a vector,old tail to overlap add (not used in first call)
- y
a vector, the convolution.
- e1
new tail to overlap add (not used in last call)
Description
Calculates the convolution y= h*x of two discrete
sequences by using the fft. The convolution is defined as follows:
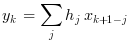
Overlap add method can be used.
USE OF OVERLAP ADD METHOD: For
x = [x1, x2,..., xNm1, xN] First call is
[y1, e1] = convol(h, x1); Subsequent calls :
[yk, ek] = convol(h, xk, ekm1); Final call :
[yN] = convol(h, xN, eNm1); Finally
y = [y1, y2,..., yNm1, yN].
The algorithm based on the convolution definition is
implemented for polynomial
product: y = convol(h, x) is equivalent
to y = coeff(poly(h,'z','c') * poly(x,'z','c')) but
much more efficient if x is a "long" array.
Examples
See also
| Report an issue | ||
| << conv2 | Convolution - intercorrélation | convol2d >> |