Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
bsplin3val
3d spline arbitrary derivative evaluation function
Syntax
[dfp]=bsplin3val(xp,yp,zp,tl,der)
Arguments
- xp, yp, zp
real vectors or matrices of same size
- tl
tlist of type "splin3d", defining a 3d tensor spline (called
sin the following)- der
vector with 3 components
[ox,oy,oz]defining which derivative ofsto compute.- dfp
vector or matrix of same format than
xp,ypandzp, elementwise evaluation of the specified derivative ofson these points.
Description
While the function interp3d may
compute only the spline s and its first derivatives,
bsplin3val may compute any derivative of
s. The derivative to compute is specified by the
argument der=[ox,oy,oz] :
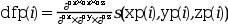
So der=[0 0 0] corresponds to
s, der=[1 0 0] to
ds/dx, der=[0 1 0] to
ds/dy, der=[1 1 0] to
d2s/dxdy, etc...
For a point with coordinates (xp(i),yp(i),zp(i)) outside the grid, the function returns 0.
Examples
deff("v=f(x,y,z)","v=cos(x).*sin(y).*cos(z)"); deff("v=fx(x,y,z)","v=-sin(x).*sin(y).*cos(z)"); deff("v=fxy(x,y,z)","v=-sin(x).*cos(y).*cos(z)"); deff("v=fxyz(x,y,z)","v=sin(x).*cos(y).*sin(z)"); deff("v=fxxyz(x,y,z)","v=cos(x).*cos(y).*sin(z)"); n = 20; // n x n x n interpolation points x = linspace(0,2*%pi,n); y=x; z=x; // interpolation grid [X,Y,Z] = ndgrid(x,y,z); V = f(X,Y,Z); tl = splin3d(x,y,z,V,[5 5 5]); // compute f and some derivates on a point // and compare with the spline interpolant xp = grand(1,1,"unf",0,2*%pi); yp = grand(1,1,"unf",0,2*%pi); zp = grand(1,1,"unf",0,2*%pi); f_e = f(xp,yp,zp) f_i = bsplin3val(xp,yp,zp,tl,[0 0 0]) fx_e = fx(xp,yp,zp) fx_i = bsplin3val(xp,yp,zp,tl,[1 0 0]) fxy_e = fxy(xp,yp,zp) fxy_i = bsplin3val(xp,yp,zp,tl,[1 1 0]) fxyz_e = fxyz(xp,yp,zp) fxyz_i = bsplin3val(xp,yp,zp,tl,[1 1 1]) fxxyz_e = fxxyz(xp,yp,zp) fxxyz_i = bsplin3val(xp,yp,zp,tl,[2 1 1])
History
| Version | Description |
| 5.4.0 | previously, imaginary part of input arguments were implicitly ignored. |
| Report an issue | ||
| << Interpolation | Interpolation | cshep2d >> |