fft
Direct or inverse Fast Fourier Transform of a vector, matrix, or hypermatrix
ifft
Inverse fast Fourier transform.
Syntax
X = fft(A) X = fft(A, sign) X = fft(A, sign, directions) X = fft(A, sign, dims, incr) X = fft(.., symmetry)
Arguments
- A, X
- vectors, matrices or ND-arrays of real or complex numbers, of same sizes.
- sign
- -1 or 1 : sign of the ±2iπ factor in the exponential term of the
transform formula, setting the direct or inverse transform. The default
value is
-1= Direct transform. - directions
- vector containing indices of
Adimensions (in [1, ndims(A)]) along which the (multidirectional) FFT must be computed. Default directions=1:ndims(A): The "cumulated" FFT is computed for all directions. See the Description section. - symmetry
- optional character string, helping fft() to choose the best algorithm:
- "symmetric": forces to consider
Aor all its "slices" as conjugate symmetric. This is useful when an exact symmetry ofAor its "slices" is possibly altered only by round-off errors. A ND-arrayBof sizes[s1,s2,..,sN]is conjugate symmetric for the FFT if and only ifB==conj(B([1 s1:-1:2],[1 s2:-1:2],...,[1 sN:-1:2])). In such a case, the resultXis real, and an efficient specific algorithm can be used to compute it. - "nonsymmetric": Then fft() does not take care of any symmetry.
- not specified: Then an automatic determination of symmetry is performed.
- "symmetric": forces to consider
- dims
- vector of positive integers. Old syntax. Each element must be a divisor of length(A). The product of the elements must be strictly smaller than length(A). See the Description section for details.
- incr
- vector of positive strictly increasing integers, as long as
dims. Old syntax. Each element must be a divisor of length(A). See the Description section for details.
Description
This function computes the direct or inverse 1D, 2D, or.. ND Discrete Fourier Transform of an array or ND-array of numbers, along one or several directions inside this one.Short syntax
Direct transform:
X = fft(A [,symmetry]) or
X = fft(A, -1 [,symmetry]) gives a direct transform.
- single variate
a=Ais a vector: a single variate direct FFT is computed, that is: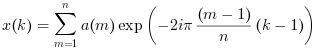
- multivariate
Ais a matrix or a multidimensional array: A multivariate direct FFT is performed.
Inverse normalized transform:
X = fft(A,+1) or X = ifft(A) performs the
inverse normalized transform, such that A==ifft(fft(A)).
- single variate
a=Ais a vector:X = fft(a, +1)orX = ifft(a)perform a single variate inverse FFT, computed as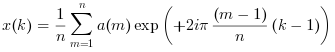
- multivariate
Ais a matrix or a multidimensional array: A multivariate inverse FFT is performed.
Long syntax : Multidimensionnal directional FFT
X = fft(A, sign, directions [, symmetry])
performs efficiently all direct or inverse FFT of all "slices" of
A along selected directions.
For example, if A is a 3D array,
X = fft(A,-1,2) is equivalent to:
and X = fft(A,-1,[1 3]) is equivalent to:
for i2 = 1:size(A,2) X(:,i2,:) = fft(A(:,i2,:), -1); end
X = fft(A, sign, dims, incr [, symmetry]) is
an old syntax that also allows to perform all direct or inverse FFT of the
slices of A along selected directions.
With this syntax, A is considered
as serialized into a vector, and its actual sizes are ignored.
The slices are selected by providing A sizes and
increments of the serialized index, related to dimensions.
For example, if A is an array with
n1*n2*n3 elements,
X = fft(A,-1, n1, 1) is equivalent to
X = fft(matrix(A,[n1,n2,n3]), -1, 1) ;
and X = fft(A,-1, [n1 n3], [1 n1*n2])
is equivalent to
X = fft(matrix(A,[n1,n2,n3]), -1, [1,3]).
Optimizing fft
Remark: The fft() function automatically stores its last internal parameters in memory to re-use them in a second time. This improves greatly the time computation when consecutive calls (with same parameters) are performed.
It is possible to go further in fft() optimization using the get_fftw_wisdom and set_fftw_wisdom functions.
Algorithms: fft() uses the fftw3 library.
Bibliography: Matteo Frigo and Steven G. Johnson, "FFTW Documentation" http://www.fftw.org/#documentation
Examples
1D FFT (of a vector):
//Frequency components of a signal //---------------------------------- // build a noised signal sampled at 1000hz containing pure frequencies // at 50 and 70 Hz sample_rate = 1000; t = 0:1/sample_rate:0.6; N = size(t,'*'); //number of samples s = sin(2*%pi*50*t) + sin(2*%pi*70*t+%pi/4) + grand(1,N,'nor',0,1); y=fft(s); // s is real so the fft response is conjugate symmetric and we retain only the first N/2 points f = sample_rate*(0:(N/2))/N; //associated frequency vector n = size(f,'*') clf() plot(f, abs(y(1:n)))
2D FFT (of a matrix):
A = zeros(256,256); A(5:24,13:17) = 1; X = fftshift(fft(A)); set(gcf(), "color_map",jet(128)); clf; grayplot(0:255, 0:255, abs(X)')
N-Dimensional FFT (of a ND array):
// simple case, 3 1-D fft at a time N = 2048; t = linspace(0,10,2048); A = [2*sin(2*%pi*3*t) + sin(2*%pi*3.5*t) 10*sin(2*%pi*8*t) sin(2*%pi*0.5*t) + 4*sin(2*%pi*0.8*t)]; X = fft(A,-1,2); fs = 1/(t(2)-t(1)); f = fs*(0:(N/2))/N; // associated frequency vector clf; plot(f(1:100)',abs(X(:,1:100))') legend(["3 and 3.5 Hz","8 Hz","0.5 and 0.8 Hz"],"in_upper_left") // 45 3-D fft at a time Dims = [5 4 9 5 6]; A = matrix(rand(1, prod(Dims)), Dims); y = fft(A,-1,[2 4 5]); // equivalent (but less efficient code) y1 = zeros(A); for i1 = 1:Dims(1) for i3 = 1:Dims(3) ind = list(i1,:,i3,:,:); y1(ind(:)) = fft(A(ind(:)),-1); end end
// Using explicit formula for 1-D discrete Fourier transform // ---------------------------------------------------------- function xf=DFT(x, Sign); n = size(x,'*'); // Compute the n by n Fourier matrix am = exp(Sign * 2*%pi*%i * (0:n-1)'*(0:n-1)/n); xf = am * matrix(x,n,1); // dft xf = matrix(xf,size(x)); // reshape if Sign == 1 then xf = xf/n; end endfunction // Comparison with the fast Fourier algorithm a = rand(1,1000); norm(DFT(a,1) - fft(a,1)) norm(DFT(a,-1) - fft(a,-1)) tic(); DFT(a,-1); toc() tic(); fft(a,-1); toc()
See also
- corr — correlation, covariance
- fftw_flags — set method for fft planner algorithm selection
- get_fftw_wisdom — return fftw wisdom
- set_fftw_wisdom — set fftw wisdom
- fftw_forget_wisdom — Reset fftw wisdom
| Report an issue | ||
| << dst | Transforms | fft2 >> |