dst
Discrete sine transform.
idst
Inverse discrete sine transform.
Syntax
X=dst(A [,sign] [,option]) X=dst(A,sign,selection [,option]) X=dst(A,sign,dims,incr [,option]) X=idst(A [,option]) X=idst(A,selection [,option]) X=idst(A,dims,incr [,option])
Arguments
- A
a real or complex vector or real or complex array (vector, matrix or N-D array.
- X
- a real or complex array with same shape as
A. - sign
- an integer. with possible values
1or-1. Select direct or inverse transform. The default value is-1(direct transform). - selection
- a vector containing index on
Aarray dimensions. See the Description part for details. - dims
- a vector of positive numbers with integer values, or a
vector of positive integers. See the Description part for details.
Each element must be a divisor of the total number of elements of
A.The product of the elements must be less than the total number of elements of
A. - incr
- a vector of positive numbers with integer values, or a
vector of positive integers. See the Description part for
details.
incrmust have the same number of elements thandims.Each element must be a divisor of the total number of elements of
A.The
increlements must be in strictly increasing order. - option
- a character string. with possible values
"dst1","dst2","dst4"or"dst"for direct transform and"dst1","dst3","dst4"or"idst"for inverse transform. The default value is"dst"for direct transform and"idst"for inverse transform. See the Description part for details.
Description
Transform description
This function realizes direct or
inverse 1-D or N-D Discrete Sine Transforms with shift depending on the
option parameter value:
For
"dst1"the function computes the unnormalized DST-I transform. The 1-D transform of a vector of length n is: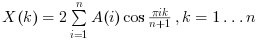
For
"dst2"the function computes the unnormalized DST-II transform. the 1-D transform of a vector of length n is: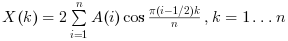
For
"dst3"the function computes the unnormalized DST-III transform. The 1-D transform of a vector of length n is: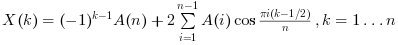
For
"dst4"the function computes the unnormalized DST-IV transform. the 1-D transform of a vector of length n is: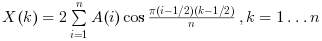
For
"dst"the function computes the normalized DST-I transform. The 1-D transform of a vector of length n is: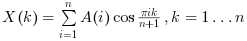
For
"idst"the function computes the normalized DST-I transform. The 1-D transform of a vector of length n is: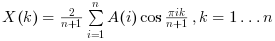
The multi-dimensional DST transforms , in general, are the separable product of the given 1d transform along each dimension of the array. For unnormalized transforms , computing the forward followed by the backward/inverse multi-dimensional transform will result in the original array scaled by the product of the dimension sizes.
Syntax description
- Short syntax
- direct
X=dst(A,-1 [,option])orX=dst(A [,option])gives a direct transform according to theoptionvalue. The default is normalized DST-I direct transform.If
Ais a vector (only one dimension greater than 1) a 1-d transform is performed and in the other cases a n-dimensional transform is done.(the
-1argument refers to the sign of the exponent..., NOT to "inverse"),- inverse
X=dst(A,1 [,option])orX=idst(A [,option])performs the inverse transform.If
Ais a vector (only one dimension greater than 1) a 1-d transform is performed and in the other cases a n-dimensional transform is done.
- Long syntax for DST along specified dimensions
X=dst(A,sign,selection [,option])allows to perform efficiently all direct or inverse dst of the "slices" ofAalong selected dimensions.For example, if
Ais a 3-D arrayX=dst(A,-1,2)is equivalent to:and
X=dst(A,-1,[1 3])is equivalent to:for i2=1:size(A,2), X(:,i2,:)=dst(A(:,i2,:),-1); end
X=dst(A,sign,dims,incr)is an old syntax that also allows to perform all direct or inverse dst of the slices ofAalong selected dimensions.For example, if
Ais an array withn1*n2*n3elementsX=dst(A,-1,n1,1)is equivalent toX=dst(matrix(A,[n1,n2,n3]),-1,1). andX=dst(A,-1,[n1 n3],[1 n1*n2])is equivalent toX=dst(matrix(A,[n1,n2,n3]),-1,[1,3]).
Optimizing dst
Remark: fftw function automatically stores his last parameters in memory to re-use it in a second time. This improves greatly the time computation when consecutives calls (with same parameters) are performed.
It is possible to go further in dst optimization using get_fftw_wisdom, set_fftw_wisdom functions.
Algorithms
This function is based on the fftw3 library.
See also
- fft — Direct or inverse Fast Fourier Transform of a vector, matrix, or hypermatrix
- dct — Discrete cosine transform.
- fftw_flags — set method for fft planner algorithm selection
- get_fftw_wisdom — return fftw wisdom
- set_fftw_wisdom — set fftw wisdom
- fftw_forget_wisdom — Reset fftw wisdom
Bibliography
Matteo Frigo and Steven G. Johnson, "FFTW Documentation" http://www.fftw.org/#documentation
| Report an issue | ||
| << dct | Transforms | fft >> |